题目内容
20．若正项等比数列{an}满足：a3+a5=4，则a4的最大值为2．分析 利用数列{an}是各项均为正数的等比数列，可得a3a5=a42，再利用基本不等式，即可求得a4的最大值．
解答 解：∵数列{an}是各项均为正数的等比数列，
∴a3a5=a42，
∵等比数列{an}各项均为正数，
∴a3+a5≥2$\sqrt{{{a}_{4}}^{2}}$，
当且仅当a3=a5=2时，取等号，
∴a3=a5=2时，a4的最大值为2．
故答案是：2．
点评 本题考查等比数列的性质，考查基本不等式的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
5．在空间，α表示平面，m，n表示二条直线，则下列命题中错误的是（ ）
| A． | 若m∥α，m、n不平行，则n与α不平行 | B． | 若m∥α，m、n不垂直，则n与α不垂直 | ||
| C． | 若m⊥α，m、n不平行，则n与α不垂直 | D． | 若m⊥α，m、n不垂直，则n与α不平行 |
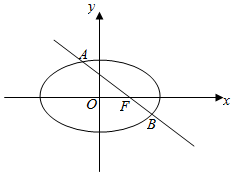椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$过点M（2，0），且右焦点为F（1，0），过F的直线l与椭圆C相交于A、B两点．设点P（4，3），记PA、PB的斜率分别为k1和k2．