题目内容
10.已知曲线x2+y=8与x轴交于A,B两点,动点P与A,B连线的斜率之积为$-\frac{1}{2}$.(1)求动点P的轨迹C的方程.
(2)MN是动点P轨迹C的一条弦,且直线OM,ON的斜率之积为$-\frac{1}{2}$.求$\overrightarrow{OM}•\overrightarrow{ON}$的最小值.
分析 (1)由已知曲线方程求出A,B的坐标,设P(x,y),结合kAPkBP=$-\frac{1}{2}$列式求得动点P的轨迹C的方程;
(2)设直线MN的方程为y=kx+m,M(x1,y1),N(x2,y2),联立直线方程与椭圆方程,由根与系数的关系结合直线OM,ON的斜率之积为$-\frac{1}{2}$可得m与k的关系,进一步求出$\overrightarrow{OM}•\overrightarrow{ON}$的范围得答案.
解答 解:(1)在方程x2+y=8中令y=0得:x=±2$\sqrt{2}$,
∴A(-2$\sqrt{2}$,0),B(2$\sqrt{2}$,0).
设P(x,y),则kAPkBP=$\frac{y}{x+2\sqrt{2}}•\frac{y}{x-2\sqrt{2}}=-\frac{1}{2}$,整理得:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$,
动点P的轨迹C的方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$;
(2)设直线MN的方程为y=kx+m,M(x1,y1),N(x2,y2),
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,得(1+2k2)x2+4kmx+2m2-8=0,
∴x1+x2=-$\frac{4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-8}{1+2{k}^{2}}$,
y1y2=(kx1+m)(kx2+m)=k2•$\frac{2{m}^{2}-8}{1+2{k}^{2}}$+km•$\frac{-4km}{1+2{k}^{2}}$+m2=$\frac{{m}^{2}-8{k}^{2}}{1+2{k}^{2}}$,
∵kOMkON=-$\frac{1}{2}$,∴$\frac{{y}_{1}}{{x}_{1}}•\frac{{y}_{2}}{{x}_{2}}=-\frac{1}{2}$,即$\frac{{m}^{2}-8{k}^{2}}{1+2{k}^{2}}=-\frac{1}{2}\frac{2{m}^{2}-8}{1+2{k}^{2}}$,
得m2=4k2+2,
∴$\overrightarrow{OM}•\overrightarrow{ON}$=x1x2+y1y2=$\frac{2{m}^{2}-8}{1+2{k}^{2}}+\frac{{m}^{2}-8{k}^{2}}{1+2{k}^{2}}=2-\frac{4}{1+2{k}^{2}}$,
∴-2≤$\overrightarrow{OM}•\overrightarrow{ON}$<2,
故$\overrightarrow{OM}•\overrightarrow{ON}$的最小值为-2.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,训练了平面向量数量积的求法,是中档题.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案| A. | 130 | B. | 170 | C. | 210 | D. | 260 |
| A. | 0 | B. | 1 | C. | -1 | D. | 1或-1 |
| A. | 在定义域内是减函数 | B. | 图象过定点(1,1) | ||
| C. | 是奇函数 | D. | 其定义域是R |
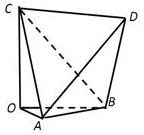 如图,多面体OABCD,AB=CD=2,AD=BC=$2\sqrt{3}$,AC=BD=$\sqrt{10}$,且OA,OB,OC两两垂直,则下列说法正确的是( )
如图,多面体OABCD,AB=CD=2,AD=BC=$2\sqrt{3}$,AC=BD=$\sqrt{10}$,且OA,OB,OC两两垂直,则下列说法正确的是( )| A. | 直线OB∥平面ACD | |
| B. | 球面经过点A、B、C、D四点的球的直径是$\sqrt{13}$ | |
| C. | 直线AD与OB所成角是45° | |
| D. | 二面角A-OC-D等于30° |

| A. | 正三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 锐角三角形 |
| A. | 3x+2y=0 | B. | x+y+1=0 | ||
| C. | x+y+1=0或3x+2y=0 | D. | x+y-1=0或3x-2y=0 |