计算${log 2}9•{log 3}5•{log {\sqrt{5}}}8$=12．题目和参考答案——青夏教育精英家教网—

题目内容

10．计算${log_2}9•{log_3}5•{log_{\sqrt{5}}}8$=12．

分析利用对数的性质、换底公式及运算法则求解．

解答解：${log_2}9•{log_3}5•{log_{\sqrt{5}}}8$
=$\frac{lg9}{lg2}×\frac{lg5}{lg3}×\frac{lg8}{lg\sqrt{5}}$
=$\frac{2lg3}{lg2}×\frac{lg5}{lg3}×\frac{3lg2}{\frac{1}{2}lg5}$
=12．
故答案为：12．

点评本题考查对数式化简求值，是基础题，解题时要认真审题，注意对数的性质、换底公式及运算法则的合理运用．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

20．若正项等比数列{a_n}满足：a₃+a₅=4，则a₄的最大值为2．

1．已知函数f（x）=$\sqrt{3}$sin²x+cos²（$\frac{π}{4}$-x）-$\frac{1+\sqrt{3}}{2}$（x∈R）．
（1）求函数f（x）在区间[0，$\frac{π}{2}$]上的最大值；
（2）在△ABC中，若A＜B，且f（A）=f（B）=$\frac{1}{2}$，求$\frac{BC}{AB}$的值．

18．如果一个数列从第2项起，每一项与它前一项的差都大于2，则称这个数列为“H型数列”．
（1）若数列{a_n}为“H型数列”，且a₁=$\frac{1}{m}$-3，a₂=$\frac{1}{m}$，a₃=4，求实数m的取值范围；
（2）是否存在首项为1的等差数列{a_n}为“H型数列”，且其前n项和S_n满足S_n＜n²+n（n∈N^*）？若存在，请求出{a_n}的通项公式；若不存在，请说明理由．
（3）已知等比数列{a_n}的每一项均为正整数，且{a_n}为“H型数列”，b_n=$\frac{2}{3}$a_n，c_n=$\frac{{a}_{n}}{（n+1）•{2}^{n-5}}$，当数列{b_n}不是“H型数列”时，试判断数列{c_n}是否为“H型数列”，并说明理由．

5．已知（0.8^1.2）^m＜（1.2^0.8）^m，则实数m的取值范围是（　　）

15．设函数$f（x）=\left\{{\begin{array}{l}{{{log}_2}x，x＞0}\\{{{log}_{0.5}}（-x），x＜0}\end{array}}\right.$．
（I）求$f（f（-\frac{1}{4}））$的值；
（II）若f（a）＞f（-a），求实数a的取值范围．

2．已知以$y=\frac{{\sqrt{6}}}{3}x$为一条渐近线的双曲线C的右焦点为$F（\sqrt{5}，0）$．
（1）求该双曲线C的标准方程；
（2）若斜率为2的直线l在双曲线C上截得的弦长为$\sqrt{6}$，求l的方程．

19．下列各组函数中，表示同一函数的是（　　）

	A．	y=x+1与y=$\frac{{x}^{2}+x}{x}$		B．	f（x）=$\frac{{x}^{2}}{（\sqrt{x}）^{2}}$与g（x）=x
	C．	$f（x）=\|x\|与g（x）=\root{n}{x^n}$		D．	$f（x）=x与g（t）={log_a}{a^t}$

14．

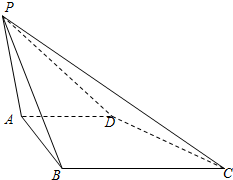如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，AB⊥BC，侧面PAD同时垂直侧面PAB与侧面PDC．若PA=AB=AD=$\frac{{\sqrt{3}}}{3}$PB，则$\frac{BC}{AD}$=$\frac{3}{2}$，直线PC与底面ABCD所成角的正切值为$\frac{\sqrt{6}}{6}$．

试题分类