题目内容
6.在长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,A1A=AD=1,求:(1)A1C与平面ABCD所成角的大小;
(2)平面A1D1DA与平面A1D1CB所成二面角的正弦值.
分析 (1)由AA1⊥平面ABCD,知∠A1CA是A1C与平面ABCD所成角,由此能求出A1C与平面ABCD所成角.
(2)由AA1⊥A1D1,A1B⊥A1D1,知∠AA1B是平面A1D1DA与平面A1D1CB所成二面角的平面角,由此能求出平面A1D1DA与平面A1D1CB所成二面角的正弦值.
解答 解:(1)∵AA1⊥平面ABCD,∴A1C在平面ABCD的射影是AC,
∴∠A1CA是A1C与平面ABCD所成角…(2分)
由AA1⊥平面ABCD,得AA1⊥AC,∴△A1CA是直角三角形,
AA1=1,AC=$\sqrt{3}$,∴A1C=$\sqrt{A{{A}_{1}}^{2}+A{C}^{2}}$=2,…(4分)
∠A1CA的对边比斜边为$\frac{1}{2}$,
∴∠A1CA=30°,
∴A1C与平面ABCD所成角为30°.…(6分)
(2)∵AA1⊥A1D1,A1B⊥A1D1,
∴∠AA1B是平面A1D1DA与平面A1D1CB所成二面角的平面角…(10分)
∵sin$∠A{A}_{1}B=\frac{AB}{{A}_{1}B}=\frac{\sqrt{2}}{\sqrt{3}}=\frac{\sqrt{6}}{3}$,
∴平面A1D1DA与平面A1D1CB所成二面角的正弦值为$\frac{\sqrt{6}}{3}$.…(12分)
点评 本题考查线面角的求法,考查二面角的正弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
7.三个数0.76,60.7,log0.7 6的大小关系为( )
| A. | log0.7 6<0.7 6<6 0.7 | B. | 0.7 6<6 0.7<log0.7 6 | ||
| C. | log0.7 6<6 0.7<0.76 | D. | 0.7 6<log0.7 6<6 0.7 |
17.函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0)的图象与x轴的交点横坐标构成一个公差为$\frac{π}{2}$的等差数列,要得到g(x)=cos(ωx+$\frac{π}{6}$)的图象,可将f(x)的图象( )
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向右平移$\frac{π}{2}$个单位 |
15.两封信随机地投入到编号为A,B,C的三个空邮筒中,则A邮筒中信件数x的数学期望E(x)等于( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{4}{9}$ |
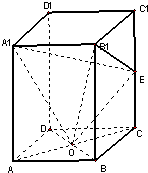 长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=8,E是CC1的中点,O是下底面正方形ABCD的中心.
长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=8,E是CC1的中点,O是下底面正方形ABCD的中心.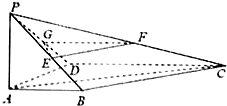 已知如图,四边形ABCD是直角梯形,AB∥DC,AB⊥AD,AP⊥平面ABCD,DC=2AB=2AD=2AP,点E、F、G分别是PB、PC、PD的中点.
已知如图,四边形ABCD是直角梯形,AB∥DC,AB⊥AD,AP⊥平面ABCD,DC=2AB=2AD=2AP,点E、F、G分别是PB、PC、PD的中点. 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.