题目内容
12.定义在[1,+∞)上的函数f(x)满足:①f(2x)=cf(x)(c为正常数);
②当2≤x≤4时,f(x)=1-|x-3|.若函数图象上所有取极大值的点均落在同一条以原点为顶点的抛物线上,则常数c=4或$\sqrt{2}$.
分析 设出原点为顶点的抛物线方程可设为x2=py(p≠0)或y2=qx(q≠0),得到$\frac{9}{p}$=($\frac{c}{4}$)n-2对n∈N*恒成立或3q=($\frac{c}{\sqrt{2}}$)n-2对n∈N*恒成立,求出c的值即可.
解答 解:记函数f(x)=cn-2(1-|$\frac{x}{{2}^{n-2}}$-3|),(2n-1≤x≤2n,n∈N*)的极大值点为pn(xn,yn).
以原点为顶点的抛物线方程可设为x2=py(p≠0)或y2=qx(q≠0).
若pn(3•2n-2,cn-2).在抛物线x2=py(p≠0)上,则(3•2n-2)2=pcn-2,
即$\frac{9}{p}$=($\frac{c}{4}$)n-2对n∈N*恒成立,从而c=4,p=9,抛物线方程为x2=9y;
若pn(3•2n-2,cn-2).在抛物线y2=qx(q≠0)上,则(cn-2)2=3q•2n-2,
即3q=($\frac{c}{\sqrt{2}}$)n-2对n∈N*恒成立,从而c=$\sqrt{2}$,q=$\frac{1}{3}$,抛物线方程为y2=$\frac{1}{3}$x,
综上:c=4或$\sqrt{2}$,
故答案为:4或$\sqrt{2}$.
点评 本小题主要考查抛物线的标准方程、利用导数研究函数的极值、不等式的解法,考查运算求解能力、化归与转化思想,是一道中档题.

练习册系列答案
相关题目
7.已知角α终边过点P(4,-3),则下列各式中正确的是( )
| A. | sinα=$\frac{3}{5}$ | B. | cosα=-$\frac{4}{5}$ | C. | tanα=-$\frac{3}{4}$ | D. | tanα=-$\frac{4}{3}$ |
17.函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0)的图象与x轴的交点横坐标构成一个公差为$\frac{π}{2}$的等差数列,要得到g(x)=cos(ωx+$\frac{π}{6}$)的图象,可将f(x)的图象( )
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向右平移$\frac{π}{2}$个单位 |
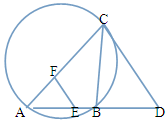 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD与点D,E,F分别为弦AB,AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD与点D,E,F分别为弦AB,AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.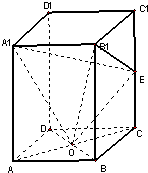 长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=8,E是CC1的中点,O是下底面正方形ABCD的中心.
长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=8,E是CC1的中点,O是下底面正方形ABCD的中心.