题目内容
18.已知数列{an}的各项均为正数,${a_1}=2,{a_{n+1}}-{a_n}=\frac{4}{{{a_{n+1}}+{a_n}}}$,若数列$\left\{{\frac{1}{{{a_{n-1}}+{a_n}}}}\right\}$的前n项和为5,则n=120.分析 先求出数列的通项公式,即可得到2$\sqrt{n+1}$=22,解得即可.
解答 解:∵数列{an}的各项均为正数,a1=2,an+1-an=$\frac{4}{{a}_{n}+{a}_{n+1}}$,
∴an+12-an2=4,
∴an+12=an2+4,
∴an+1=$\sqrt{4+{a}_{n}^{2}}$
∵a1=2,
∴a2=$\sqrt{4+4}$=2$\sqrt{2}$,
∴a3=$\sqrt{4+8}$=2$\sqrt{3}$,
a4=$\sqrt{4+12}$=2$\sqrt{4}$,
…
由此猜想an=2$\sqrt{n}$.
∵${a_1}=2,{a_{n+1}}-{a_n}=\frac{4}{{{a_{n+1}}+{a_n}}}$,若数列$\left\{{\frac{1}{{{a_{n-1}}+{a_n}}}}\right\}$的前n项和为5,
∴$\frac{1}{4}$(a2-a1+a3-a2+…+an+1-an)=$\frac{1}{4}$(an+1-2)=5
∴2$\sqrt{n+1}$=22
解得n+1=121,
∴n=120.
故答案为:120.
点评 本题考查实数值的求法,是中档题,解题时要认真审题,注意数列的递推公式、累加法的合理运用.

练习册系列答案
相关题目
6.下列函数中,既是奇函数,又在区间(0,+∞)上为增函数的是( )
| A. | f(x)=x2-x | B. | f(x)=$\frac{1}{x}$+x | C. | f(x)=2x+$\frac{1}{{2}^{x}}$ | D. | f(x)=x|x| |
7.三个数0.76,60.7,log0.7 6的大小关系为( )
| A. | log0.7 6<0.7 6<6 0.7 | B. | 0.7 6<6 0.7<log0.7 6 | ||
| C. | log0.7 6<6 0.7<0.76 | D. | 0.7 6<log0.7 6<6 0.7 |
17.函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0)的图象与x轴的交点横坐标构成一个公差为$\frac{π}{2}$的等差数列,要得到g(x)=cos(ωx+$\frac{π}{6}$)的图象,可将f(x)的图象( )
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向右平移$\frac{π}{2}$个单位 |
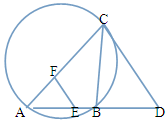 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD与点D,E,F分别为弦AB,AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD与点D,E,F分别为弦AB,AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.