题目内容
若不等式ax2-bx-1≥0的解集为[-
,-
],则不等式x2-bx-a<0的解集为 .
| 1 |
| 2 |
| 1 |
| 3 |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:不等式ax2-bx-1≥0的解集为[-
,-
],可得-
,-
是一元二次方程ax2-bx-1=0的两个实数根,且a<0.利用根与系数的关系即可得出.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
解答:
解:∵不等式ax2-bx-1≥0的解集为[-
,-
],∴-
,-
是一元二次方程ax2-bx-1=0的两个实数根,且a<0.
∴
,解得a=-6,b=5.
则不等式x2-bx-a<0化为x2-5x+6<0,即(x-2)(x-3)<0,解得2<x<3.
∴不等式x2-bx-a<0的解集为(2,3).
故答案为:(2,3).
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∴
|
则不等式x2-bx-a<0化为x2-5x+6<0,即(x-2)(x-3)<0,解得2<x<3.
∴不等式x2-bx-a<0的解集为(2,3).
故答案为:(2,3).
点评:本题考查了一元二次不等式的解法、一元二次方程的根与系数的关系,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知p:|x-2|≤3,q:-1≤x≤5,则p是q的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
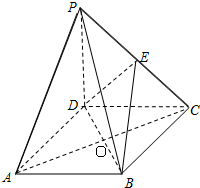 如图,在四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是边长为a的正方形,对角线AC与BD相交于O,且PD=a,E为棱PC的中点.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是边长为a的正方形,对角线AC与BD相交于O,且PD=a,E为棱PC的中点.