题目内容
若tanα=-
，则
= ．
| 1 |
| 2 |
| 1 |
| 2sinαcosα-sin2α |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：利用同角三角函数基本关系的运用，将弦化切即可求得答案．
解答：
解：∵tanα=-
，
∴
=
=
=
=-1，
故答案为：-1．
| 1 |
| 2 |
∴
| 1 |
| 2sinαcosα-sin2α |
| cos2α+sin2α |
| 2sinαcosα-sin2α |
| 1+tan2α |
| 2tanα-tan2α |
1+
| ||
-1-
|
故答案为：-1．
点评：本题考查同角三角函数基本关系的运用，分子中的1化为sin2α+cos2α，再将“弦”化“切”是关键，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
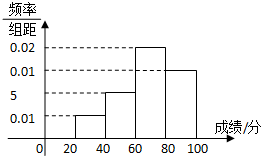学校组织学生参加模块测试，测试后随机抽查部分学生的成绩，成绩的频率分布直方图如图5，数据的分组依次为[20，40），[40，60），[60，80），[80，100]，低于60分的人数是6人