题目内容
已知x≥1，y≥1，求证：x2y+xy2+1≤x2y2+x+y．
考点：二维形式的柯西不等式
专题：证明题,不等式
分析：左边-右边，利用x≥1，y≥1，即可得出结论．
解答：
证明：左边-右边=（y-y2）x+（y2-1）x-y+1=（1-y）[yx2-（1+y）x+1]…（4分）
=（1-y）（xy-1）（x-1），…（6分）
∵x≥1，y≥1，
∴1-y≤0，xy-1≥0，x-1≥0． …（8分）
从而左边-右边≤0，
∴x2y+xy2+1≤x2y2+x+y． …（10分）
=（1-y）（xy-1）（x-1），…（6分）
∵x≥1，y≥1，
∴1-y≤0，xy-1≥0，x-1≥0． …（8分）
从而左边-右边≤0，
∴x2y+xy2+1≤x2y2+x+y． …（10分）
点评：本题考查不等式的证明，考查作差法，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
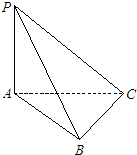如图，已知PA⊥平面ABC，AB⊥BC，若PA=2，AB=1，BC=
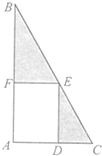某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地，如图，A=