题目内容

19．如果二次函数y=ax2+（b-3）x+c（a≠0）是偶函数，则b=3．

分析 根据二次函数的对称性，得其对称轴是y轴，从而求得b．

解答 解：由题意，可知二次函数的图象关于y轴对称，
则对称轴为x=-$\frac{b-3}{2a}$=0，
则b=3，
故答案为：3．

点评 本题考查二次函数的基本性质，对称性与函数的对称轴的关系．

练习册系列答案
相关题目
9．已知a、b∈R，比较|a|+$\frac{|b|}{2}$与$\sqrt{2}$•$\sqrt{|ab|}$的大小．
10．已知：x=$\frac{1}{2}$（$\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}}$）（a＞0，b＞0），求$\frac{2b\sqrt{{x}^{2}-1}}{x-\sqrt{{x}^{2}-1}}$的值．
7．已知集合M={f（x）|f（x）=$\frac{1}{\sqrt{1-x}}$}，N={g（x）|g（x）=ln（x+1）}，则M∩N=（　　）
A．（1，1）B．（0，+∞）C．（1，+∞）D．（-∞，1）
14．已知函数f（x）=$\frac{{x}^{2}+2x+a}{x}$，x∈[1，+∞）．
（1）当a=$\frac{1}{2}$时，用定义探讨函数f（x）在x∈[1，+∞）上的单调性并求f（x）最小值；
（2）若对任意x∈[1，+∞），f（x）＞0恒成立，试求实数a的取值范围．
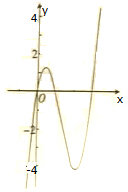4．已知函数f（x）=2x（x-1）（x-3）的图象如图所示，有以下关于方程f（x）+1=0的说法：①有2个实数根；②当x＞0时，有1个实数根；③当-1＜x＜0时，有1个实数根；④当x＞1时，有1个实数根；⑤当-1＜x＜3时，有3个实数根．其中正确说法的序号是③⑤（填上所有正确命题的序号）．
11．y=2x-1的定义域是（　　）
A．（-∞，+∞）B．（1，+∞）C．[1，+∞）D．（0，1）∪（1，+∞）
11．设数列{an}的前n项和为Sn，且a1=-1，an+1=Sn+1Sn，则Sn=-$\frac{1}{n}$．
12．方程$2sin（x+\frac{π}{3}）$+a-1=0在[0，π]上有两个不等的实根，则实数a的取值范围是$（-1，1-\left.{\sqrt{3}}]$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网