题目内容
12.方程$2sin(x+\frac{π}{3})$+a-1=0在[0,π]上有两个不等的实根,则实数a的取值范围是$(-1,1-\left.{\sqrt{3}}]$.分析 由题意可得y=2sin(x+$\frac{π}{3}$)的图象和直线y=1-a在[0,π]上有两个不同的交点,数形结合可得a的范围.
解答 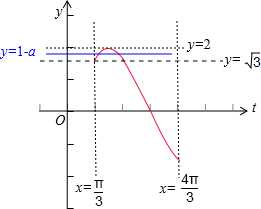 解:方程$2sin(x+\frac{π}{3})$+a-1=0在[0,π]上有两个不等的实根,
解:方程$2sin(x+\frac{π}{3})$+a-1=0在[0,π]上有两个不等的实根,
即y=2sin(x+$\frac{π}{3}$)的图象和直线y=1-a在[0,π]上有两个不同的交点.
∵x∈[0,π],∴x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{4π}{3}$],令t=x+$\frac{π}{3}$,
则y=2sint的图象和直线y=1-a在[$\frac{π}{3}$,$\frac{4π}{3}$]上有两个不同的交点.
如图所示:
故有$\sqrt{3}$≤1-a<2,求得-1<a≤1-$\sqrt{3}$,
故答案为:$(-1,1-\left.{\sqrt{3}}]$.
点评 本题主要考查正弦函数的图象特征,方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
3.下列说法错误的是( )
| A. | “由直线与圆相切时,圆心与切点连线与该直线垂直,想到平面与球相切时,球心与切点连线与该平面垂直”,以上推理运用的是类比推理 | |
| B. | 命题“?x∈R,x2-2x+4≤0”的否定为“?x∈R,x2-2x+4>0” | |
| C. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| D. | 用反证法证明命题“设a,b为实数,则方程x2+ax+b=0至多有一个实根”时,要做的假设是“方程x2+ax+b=0至少有一个实根” |
7.数列{an}满足a1=0,an+1=$\frac{{a}_{n}-2}{\frac{5}{4}{a}_{n}-2}$,则a2015=( )
| A. | 0 | B. | $\frac{4}{3}$ | C. | 1 | D. | 2 |
17.已知平面a和直线l,则a内至少有一条直线与l( )
| A. | 平行 | B. | 相交 | C. | 垂直 | D. | 异面 |