题目内容
下列各组中的两个函 数是同一函数的是( )
(1)y1=
;y2=x-5;
(2)y1=
,y2=
;
(3)f (x)=x,g(x)=
;
(4)f(x)=
,F(x)=x3
;
(5)f1(x)=(
)2,f2(x)=2x-5.
(1)y1=
| (x-3)(x+5) |
| x+3 |
(2)y1=
| x+1 |
| x-1 |
| (x+1)(x-1) |
(3)f (x)=x,g(x)=
| x2 |
(4)f(x)=
| 3 | x4-x3 |
| x-1 |
(5)f1(x)=(
| 2x-5 |
| A、(1)(2) |
| B、(2)(3) |
| C、(4) |
| D、(3)(5) |
考点:判断两个函数是否为同一函数
专题:函数的性质及应用
分析:判断两个函数的定义域以及对应法则是否相同,即可得到结果.
解答:
解:对于(1),y1=
的定义域是{x|x∈R且x≠-3},y2=x-5的定义域是R,两个函数的定义域不相同不是相同函数;
对于(2),y1=
的定义域是{x|x≥1},y2=
的定义域是{x|x≤-1,或x≥1},两个函数的定义域不相同不是相同函数;
对于(3),f (x)=x,g(x)=
的定义域均是R,但g(x)=
=|x|,两个函数对应关系不相同,不是相同的函数;
对于(4),f(x)=
=x3
,F(x)=x3
;两个函数的定义域均为R,对应法则相同,是相同的函数;
对于(5),函数f1(x)=(
)2的定义域为{x|x≥
},f2(x)=2x-5的定义域为R,不是相同的函数;
故只有第(4)组的两个函数是同一函数,
故选:C.
| (x-3)(x+5) |
| x+3 |
对于(2),y1=
| x+1 |
| x-1 |
| (x+1)(x-1) |
对于(3),f (x)=x,g(x)=
| x2 |
| x2 |
对于(4),f(x)=
| 3 | x4-x3 |
| x-1 |
| x-1 |
对于(5),函数f1(x)=(
| 2x-5 |
| 5 |
| 2 |
故只有第(4)组的两个函数是同一函数,
故选:C.
点评:本题考查两个函数是否相同的判定,注意两个函数相同条件:定义域与对应法则相同.基本知识的考查.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
已知a,b,c∈R,则“abc<0”是ax2+by2=c表示双曲线的 ( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充分必要 |
| D、既不充分也不必要 |
设集合S={x|x2-2x=0x∈R},T={x|x2+2x-3≤0,x∈R},则S∩T=( )
| A、{0,2} |
| B、{0} |
| C、{0,-2} |
| D、{2,0,-2} |
命题p:?x∈(0,
),3sinx-πx<0,则?p( )
| π |
| 2 |
A、?x∈(0,
| ||
B、?x0∈(0,
| ||
C、?x∈(0,
| ||
D、?x0∈(0,
|
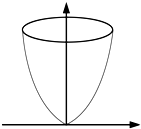 抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是
抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是