题目内容
命题p：?x∈（0，
），3sinx-πx＜0，则?p（ ）
| π |
| 2 |
A、?x∈（0，
| ||
B、?x0∈（0，
| ||
C、?x∈（0，
| ||
D、?x0∈（0，
|
考点：命题的否定
专题：简易逻辑
分析：直接利用全称命题的否定是特称命题写出结果即可．
解答：
解：因为全称命题的否定是特称命题，所以命题p：?x∈（0，
），3sinx-πx＜0，
则?p：?x0∈（0，
），3sinx0-πx0≥0．
故选：D．
| π |
| 2 |
则?p：?x0∈（0，
| π |
| 2 |
故选：D．
点评：本题考查命题的否定，全称命题与特称命题的否定关系，基本知识的考查．
练习册系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
在△ABC中，a，b，c分别是角A，B，C的对边，若a2=b2+bc+c2，则A=（ ）
| A、30° | B、60° |
| C、120° | D、150° |
下列各组中的两个函 数是同一函数的是（ ）
（1）y1=
；y2=x-5；
（2）y1=
，y2=
；
（3）f （x）=x，g（x）=
；
（4）f（x）=
，F（x）=x3
；
（5）f1（x）=（
）2，f2（x）=2x-5．
（1）y1=
| (x-3)(x+5) |
| x+3 |
（2）y1=
| x+1 |
| x-1 |
| (x+1)(x-1) |
（3）f （x）=x，g（x）=
| x2 |
（4）f（x）=
| 3 | x4-x3 |
| x-1 |
（5）f1（x）=（
| 2x-5 |
| A、（1）（2） |
| B、（2）（3） |
| C、（4） |
| D、（3）（5） |
已知集合A={（x，y）|x+y=2}，B={（x，y）x-y=4}那么集合A∩B为（ ）
| A、{（-1，3）} |
| B、（3，-1） |
| C、{3，-1} |
| D、{（3，-1）} |
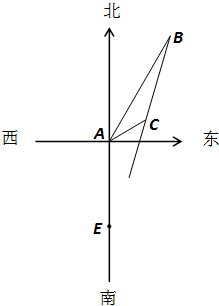在一个特定时段内，以点E为中心的7海里以内海域被设为警戒水域．点E正北55海里处有一个雷达观测站A．某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40