题目内容
2.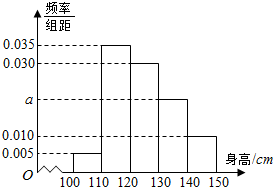 从某小学所有学生中随机抽取100名学生,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),其中样本数据分组[100,110),[110,120),[120,130),[130,140),[140,150),若要从身高在),[120,130),[130,140),[140,150)三组内的学生中,用分层抽样的方法抽取12人参加一项活动,则从身高在[130,140)内的学生中抽取的人数应为4.
从某小学所有学生中随机抽取100名学生,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),其中样本数据分组[100,110),[110,120),[120,130),[130,140),[140,150),若要从身高在),[120,130),[130,140),[140,150)三组内的学生中,用分层抽样的方法抽取12人参加一项活动,则从身高在[130,140)内的学生中抽取的人数应为4.
分析 由频率分布直方图,先求出身高在[130,140)内的频率,由此能求出从身高在[130,140)内的学生中抽取的人数.
解答 解:由频率分布直方图,得身高在[130,140)内的频率为:
1-(0.005+0.010+0.030+0.035)×10=0.2,
所以身高在[120,130),[130,140),[140,150)三组频率分别为0.3,0.2,0.1,
故三组的人数比为3:2:1
∴用分层抽样的方法从三组选取12人参加一项活动,
从身高在[130,140)内的学生中抽取的人数应为:
12×$\frac{2}{6}$=4.
故答案为:4.
点评 本题考查频率分布直方图的应用,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
13.已知点Q(2$\sqrt{2}$,0)及抛物线x2=4y上一动点P(x,y),则y+|PQ|的最小值是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
17.若一个底面是正三角形且侧棱垂直于底面的三棱柱的正(主)视图如图所示,则其侧面积等于( )


| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
14.在等比数列{an}中,a1=1,则“a2=4”是“a3=16”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
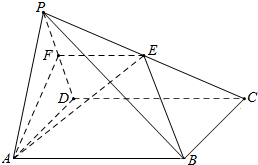 如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.