题目内容
11．在平行四边形ABCD中，已知AB=4，AD=3，∠DAB=$\frac{π}{3}$，点E，F分别在边AD，BC上，且$\overrightarrow{AD}$=3$\overrightarrow{AE}$，$\overrightarrow{BF}$=2$\overrightarrow{FC}$，则$\overrightarrow{AB}$•$\overrightarrow{EF}$的值为18．分析 运用数量积的定义可得$\overrightarrow{AB}$•$\overrightarrow{AD}$=6，再由向量的加减运算，可得$\overrightarrow{EF}$=$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AD}$，再由数量积的性质：
向量的平方即为模的平方，可得所求值．
解答 
解：$\overrightarrow{AB}$•$\overrightarrow{AD}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|•cos$\frac{π}{3}$=4×3×$\frac{1}{2}$=6，
$\overrightarrow{EF}$=$\overrightarrow{AF}$-$\overrightarrow{AE}$=$\overrightarrow{AB}$+$\overrightarrow{BF}$-$\frac{1}{3}$$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AD}$-$\frac{1}{3}$$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AD}$，
即有$\overrightarrow{AB}$•$\overrightarrow{EF}$=$\overrightarrow{AB}$•（$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AD}$）
=$\overrightarrow{AB}$2+$\frac{1}{3}$$\overrightarrow{AB}$•$\overrightarrow{AD}$=16+$\frac{1}{3}$×6=18．
故答案为：18．
点评 本题主要考查两个向量的数量积的定义，两个向量的加减法的法则，以及数量积的性质，体现了数形结合的数学思想，属于中档题．
通城学典默写能手系列答案
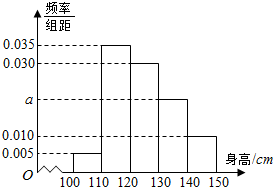从某小学所有学生中随机抽取100名学生，将他们的身高（单位：cm）数据绘制成频率分布直方图（如图），其中样本数据分组[100，110），[110，120），[120，130），[130，140），[140，150），若要从身高在），[120，130），[130，140），[140，150）三组内的学生中，用分层抽样的方法抽取12人参加一项活动，则从身高在[130，140）内的学生中抽取的人数应为4．| A． | （0，2] | B． | （0，2） | C． | {1，2} | D． | {0，1，2} |
| A． | 7 | B． | 9 | C． | 11 | D． | 12 |
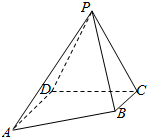如图，四棱锥P-ABCD中，平面PCD⊥平面ABCD，△PCD是等边三角形，四边形ABCD是梯形，BC∥AD，BC⊥CD，AD=2BC=2$\sqrt{2}$．