题目内容
12．若椭圆的对称轴为坐标轴，长轴长与短轴长的和为18，焦距为6，（1）求这个椭圆的离心率；
（2）求这个椭圆的标准方程．
分析 （1）利用已知条件求出椭圆的几何量，然后求解椭圆的离心率．
（2）利用椭圆的几何量写出椭圆的标准方程即可．
解答 解：由题知：2a+2b=18，且2c=6，由于a2=b2+c2，得a=5，b=4，c=3，所以
（1）离心率为e=$\frac{c}{a}$=$\frac{3}{5}$．
（2）椭圆方程为$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$或$\frac{{y}^{2}}{25}+\frac{{x}^{2}}{16}=1$．
点评 本题考查椭圆简单性质的应用，椭圆的标准方程的求法，是基础题．
练习册系列答案
相关题目
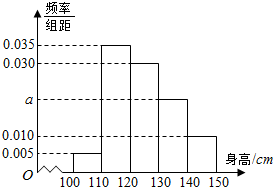从某小学所有学生中随机抽取100名学生，将他们的身高（单位：cm）数据绘制成频率分布直方图（如图），其中样本数据分组[100，110），[110，120），[120，130），[130，140），[140，150），若要从身高在），[120，130），[130，140），[140，150）三组内的学生中，用分层抽样的方法抽取12人参加一项活动，则从身高在[130，140）内的学生中抽取的人数应为4．
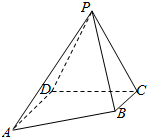如图，四棱锥P-ABCD中，平面PCD⊥平面ABCD，△PCD是等边三角形，四边形ABCD是梯形，BC∥AD，BC⊥CD，AD=2BC=2$\sqrt{2}$．
7．全称命题：?x∈R，x2≤0的否定是（ ）
| A． | ?x∈R，x2≤0 | B． | ?x0∈R，x${\;}_{0}^{2}$＞0 | C． | ?x0∈R，x${\;}_{0}^{2}$＜0 | D． | ?x0∈R，x${\;}_{0}^{2}$≤0 |