题目内容
14．在等比数列{an}中，a1=1，则“a2=4”是“a3=16”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合等比数列的性质进行求解即可．
解答 解：在等比数列{an}中，a1=1，若a2=4，则公比q=$\frac{{a}_{2}}{{a}_{1}}=\frac{4}{1}=4$，则a3=a2q=4×4=16．
若a3=16，则a3=1×q2=16，即q=±4，
当q=-4时，a2=a1q=-4，此时a2=4不成立，
即“a2=4”是“a3=16”的充分不必要条件，
故选：A．
点评 本题主要考查充分条件和必要条件的判断，根据等比数列的通项公式求出公比是解决本题的关键．
练习册系列答案
相关题目
4．若方程2ax2-x-1=0在（0，1）内恰有一个零点，则有（ ）
| A． | a＜-1 | B． | a＞1 | C． | -1＜a＜1 | D． | 0≤a＜1 |
5．已知A，B为圆C：（x-m）2+（y-n）2=9（m，n∈R）上两个不同的点（C为圆心），且满足$|\overrightarrow{CA}+\overrightarrow{CB}|=\sqrt{13}$，则|AB|=（ ）
| A． | $\sqrt{23}$ | B． | $\frac{{\sqrt{23}}}{2}$ | C． | 2 | D． | 4 |
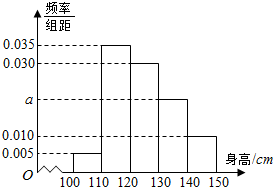从某小学所有学生中随机抽取100名学生，将他们的身高（单位：cm）数据绘制成频率分布直方图（如图），其中样本数据分组[100，110），[110，120），[120，130），[130，140），[140，150），若要从身高在），[120，130），[130，140），[140，150）三组内的学生中，用分层抽样的方法抽取12人参加一项活动，则从身高在[130，140）内的学生中抽取的人数应为4．
6．设集合M={x||2x-1|≤3}，N={x∈Z|1＜2x＜8}，则M∩N=（ ）
| A． | （0，2] | B． | （0，2） | C． | {1，2} | D． | {0，1，2} |
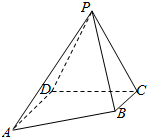如图，四棱锥P-ABCD中，平面PCD⊥平面ABCD，△PCD是等边三角形，四边形ABCD是梯形，BC∥AD，BC⊥CD，AD=2BC=2$\sqrt{2}$．