题目内容
16.数列{an}中,2Sn=n2+n.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=2an•an,求数列{bn}的前n项和Tn.
分析 (I)利用递推关系即可得出.
(II)bn=2an•an=n•2n.“错位相减法”、等比数列的通项公式及其前n项和公式即可得出.
解答 解:(I)∵2Sn=n2+n,∴n=1时,2a1=1+1,解得a1=1.n≥2时,2an=2(Sn-Sn-1)=n2+n-[(n-1)2+(n-1)],化为:an=n.n=1时也成立,
∴an=n.
(II)bn=2an•an=n•2n.
∴数列{bn}的前n项和Tn=2+2×22+3×23+…+n•2n,
∴2Sn=22+2×23+…+(n-1)•2n+n•2n+1,
∴-Sn=2+22+…+2n-n•2n+1=$\frac{2({2}^{n}-1)}{2-1}$-n•2n+1=(1-n)•2n+1-2,
∴Sn=(n-1)•2n+1+2.
点评 本题考查了“错位相减法”、等比数列的通项公式及其前n项和公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
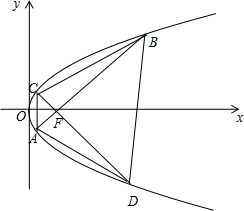 如图,在直角坐标系xOy中,点P(1,2)到抛物线E:y2=2px(p>0)的焦点的距离为$\sqrt{5}$,过抛物线E的焦点F作两条相互垂直的直线分别交抛物线于A,B,C,D四点.
如图,在直角坐标系xOy中,点P(1,2)到抛物线E:y2=2px(p>0)的焦点的距离为$\sqrt{5}$,过抛物线E的焦点F作两条相互垂直的直线分别交抛物线于A,B,C,D四点.