已知函数f(x)=$\left\{\begin{array}{l}{lo{g} {2}(4-x).x＜4}\\{1+{2}^{x-1}.x≥4}\end{array}\right.$.则f(0)+f(log232)=( )A．19B．17C．15D．13 题目和参考答案——青夏教育精英家教网—

题目内容

3．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}（4-x），x＜4}\\{1+{2}^{x-1}，x≥4}\end{array}\right.$，则f（0）+f（log₂32）=（　　）

A．

B．

C．

D．

分析利用函数的解析式，真假求解函数值即可．

解答解：函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}（4-x），x＜4}\\{1+{2}^{x-1}，x≥4}\end{array}\right.$，
则f（0）+f（log₂32）=log₂4+1+${2}^{lo{g}_{2}32-1}$=2+1+$\frac{1}{2}×32$=19．
故选：A．

点评本题考查分段函数的应用，函数值的求法，考查计算能力．

练习册系列答案

相关题目

1．

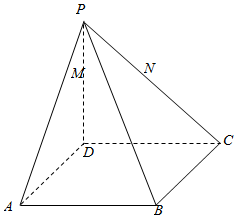如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，M，N分别为PD，PC上的点，且$\frac{PM}{MD}$=$\frac{PN}{NC}$，求证：MN∥AB．

2．设x，y为实数，若4x²+2xy+3y²=1，则2x-y的最大值和最小值，并说明取得最值时的条件．

11．数列{a_n}满足：2a₁+2²a₂+2³a₃+…+2ⁿa_n=（n+1）²（n∈N^*），则数列{a_n}的前n项和为 S_n=$\frac{11}{2}$-$\frac{2n+5}{{2}^{n}}$．

18．圆（x-2）²+y²=5与直线y=2x+1的位置关系是（　　）

8．

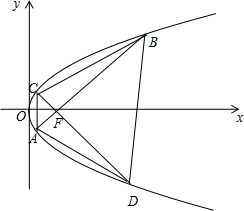如图，在直角坐标系xOy中，点P（1，2）到抛物线E：y²=2px（p＞0）的焦点的距离为$\sqrt{5}$，过抛物线E的焦点F作两条相互垂直的直线分别交抛物线于A，B，C，D四点．
（1）求抛物线C的方程；
（2）求四边形ACBD面积的最小值．

15．已知复数z满足z-i=iz+3，则$\overline{z}$=（　　）

12．

在如图所示的五面体中，四边形ABCD是矩形，平面ADF⊥平面ABEF，且AB∥EF，AB=$\frac{1}{2}$EF=2$\sqrt{2}$，AF=BE=2，M是EF的中点，N在AM上．
（I）求证：DN∥平面BCE；
（Ⅱ）求证：平面ABEF⊥平面ABCD．

13．已知函数f（x）=$\left\{\begin{array}{l}{sinx+2cos2x，x≥0}\\{-{e}^{2x}，x＜0}\\{\;}\end{array}\right.$，则f（f（$\frac{π}{2}$））等于（　　）

-e²

e²

试题分类