题目内容
在可行域
,使得目标函数z=2x-4y,取得最大值的最优解为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z的几何意义,即可求出最优解.
解答:
 解:作出不等式组
解:作出不等式组
对应的平面区域如图:
z=2x-4y,则y=
x-
z,
平移直线z=2x-4y,由图象可知当直线y=
x-
z与x-2y=0重合时,直线y=
x-
z的截距最小,此时z最大,
故取得最大值时的最优解为线段OA,即x-2y=0,x∈[0,2]
故答案为:x-2y=0,x∈[0,2].
 解:作出不等式组
解:作出不等式组
|
z=2x-4y,则y=
| 1 |
| 2 |
| 1 |
| 4 |
平移直线z=2x-4y,由图象可知当直线y=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
故取得最大值时的最优解为线段OA,即x-2y=0,x∈[0,2]
故答案为:x-2y=0,x∈[0,2].
点评:本题主要考查线性规划的应用,利用z的几何意义,结合数形结合是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若直线a与平面α不垂直,那么平面α内与直线a垂直的直线有( )
| A、0条 | B、1条 |
| C、无数条 | D、不确定 |
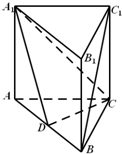 如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,∠ACB=90°,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,∠ACB=90°,点D是AB的中点.