题目内容
已知正方形的边长为2
,中心为(-3,-4),一边与直线2x+y+3=0平行,求正方形的各边所在直线方程.
| 5 |
考点:直线的点斜式方程
专题:直线与圆
分析:设其中两条的直线方程为:2x+y+c1=0,2x+y+c2=0,由题意可得
=
=
,解得c1=5,c2=15,可得直线方程,同理设另外两条直线方程为:x-2y+c3=0,x-2y+c4=0,求得c3和c4可得答案.
| |-6-4+c1| | ||
|
| |-6-4+c2| | ||
|
| 5 |
解答:
解:由正方形的特点和平行关系设其中两条的直线方程为:2x+y+c1=0,2x+y+c2=0,
∵正方形的边长为2
且正方形的中心为(-3,-4),
∴
=
=
,解得c1=5,c2=15,
∴这两条直线的方程为:2x+y+15=0,2x+y+5=0,
又由垂直关系可设另外两条直线方程为:x-2y+c3=0,x-2y+c4=0,
同理可得
=
=
,解得c3=0,c4=-10,
∴这两条直线的方程为:x-2y=0,x-2y-10=0,
∴该正方形的各边所在直线方程2x+y+15=0,2x+y+5=0,x-2y=0,x-2y-10=0.
∵正方形的边长为2
| 5 |
∴
| |-6-4+c1| | ||
|
| |-6-4+c2| | ||
|
| 5 |
∴这两条直线的方程为:2x+y+15=0,2x+y+5=0,
又由垂直关系可设另外两条直线方程为:x-2y+c3=0,x-2y+c4=0,
同理可得
| |-3+8+c3| | ||
|
| |-3+8+c4| | ||
|
| 5 |
∴这两条直线的方程为:x-2y=0,x-2y-10=0,
∴该正方形的各边所在直线方程2x+y+15=0,2x+y+5=0,x-2y=0,x-2y-10=0.
点评:本题考查直线方程,涉及平行和垂直关系以及点到直线的距离公式,属中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
设等差数列{an}的前n项和为Sn,若
=
,则
=( )
| S5 |
| S10 |
| 1 |
| 3 |
| S5 |
| S20 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知直线l1的方向向量
=(1.1,1),直线l2的方向向量
=(-2.2,-2),则l1,l2夹角的余弦值为( )
| s1 |
| s2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
设变量x,y满足约束条件
,则
的最大值为( )
|
| y |
| x |
A、
| ||
| B、1 | ||
| C、2 | ||
D、
|
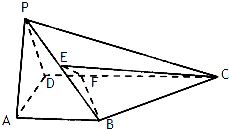 如图,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,△PAD是边长为
如图,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,△PAD是边长为