题目内容

6．下列四个图象中，不能作为函数图象的是（　　）
A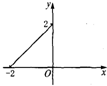．B．C．D．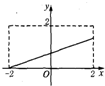

分析 根据函数的定义可知函数须满足“自变量x的任意性”，“函数值y的唯一性”，据此可得函数图象的特征，由此可得答案．

解答 解：由函数的定义可知，对定义域内的任意一个自变量x的值，都有唯一的函数值y与其对应，
故函数的图象与直线x=a至多有一个交点，
图C中，当-2＜a＜2时，x=a与函数的图象有两个交点，不满足函数的“唯一性”，故C不是函数的图象，
故选：C

点评 本题考查函数的定义及其图象特征，准确理解函数的“任意性”和“唯一性”是解决该题的关键．

练习册系列答案
相关题目
8．一个几何体的三视图如图所示，则这个几何体的体积为（　　）
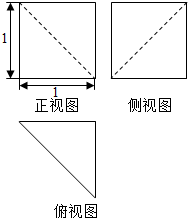
A．$\frac{5}{6}$B．$\frac{1}{2}$C．$\frac{1}{3}$D．$\frac{1}{6}$
17．在等差数列{an}中，若a3和a9是方程x2-4x+3=0的两根，则a6的值是2．
14．设点P（x，y）是曲线a|x|+b|y|=1（a≥0，b≥0）上任意一点，其坐标（x，y）均满足$\sqrt{{x^2}+{y^2}+4x+4}+\sqrt{{x^2}+{y^2}-4x+4}≤8$，则$2a+\sqrt{3}b$的取值范围为[1，+∞）．
1．已知关于x方程|x2+2x-3|=a（a∈R）有两个实数解，则a的取值范围是a=0，或a＞4，．
11．若奇函数f（x）在区间[4，9]上是减函数且最小值为2，则f（x）在区间[-9，-4]上是（　　）
A．增函数且最大值为-2B．增函数且最小值为-2
C．减函数且最小值为-2D．减函数且最大值为-2
18．已知点A（2，1）与圆C：（x-1）2+（y-2）2=3，则点A与圆C的位置关系为点在圆内．
15．定义在R上的偶函数f（x），对任意x∈R，均有f（x+4）=f（x）成立，当x∈[0，2]时，f（x）=2x+1，则直线y=4与y=f（x）的图象交点中最近两点的距离为1．
16．设x，y满足约束条件$\left\{\begin{array}{l}{3x-y-2≤0}\\{x-y≥0}\\{x≥0，y≥0}\end{array}\right.$，若目标函数z=x+$\frac{m}{2}$y（m＞0）的最大值为2，
则y=sin（mx+$\frac{π}{3}$）的图象向右平移$\frac{π}{6}$后的表达式为y=sin2x．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网