题目内容
15.定义在R上的偶函数f(x),对任意x∈R,均有f(x+4)=f(x)成立,当x∈[0,2]时,f(x)=2x+1,则直线y=4与y=f(x)的图象交点中最近两点的距离为1.分析 先求出函数的周期,然后根据偶函数图象的性质画出函数的部分图象,结合图形进行求解即可.
解答  解:∵对任意的x∈R均有f(x+4)=f(x)成立,
解:∵对任意的x∈R均有f(x+4)=f(x)成立,
∴y=f(x)的周期为4,
而y=f(x)为偶函数,图象关于y轴对称.
画出函数的图象,
将y=4代入f(x)=2x+1解得x=$\frac{3}{2}$,
根据图形可知图象关于x=2对称,则在[2,4]上的交点横坐标为$\frac{5}{2}$
∴直线y=4与函数y=f(x)的图象交点中最近两点的距离等于1.
故答案为:1
点评 本题主要考查了函数的周期性与偶函数图象的性质,同时考查了数形结合的思想,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
6.下列四个图象中,不能作为函数图象的是( )
| A. | 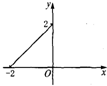 | B. |  | C. |  | D. | 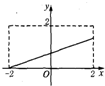 |
3.已知2x2+x-3=(x-1)(ax+b),则a,b的值分别为( )
| A. | 2,3 | B. | 2,-3 | C. | -2,3 | D. | -2,-3 |
10.下列说法正确的是( )
| A. | 相关关系与函数关系都是一种确定关系,也是一种因果关系 | |
| B. | 某同学研究卖出的热饮杯数y与气温x之间的关系,得到回归方程$\widehat{y}$=-2.352x+147.767,则气温为2摄氏度时,一定可卖出143杯热饮 | |
| C. | 相关系数|r|越大时相关性越强 | |
| D. | 相关系数|r|越大时相关性越弱 |
20.对于下列四个命题
p1:?x∈(0,+∞),($\frac{1}{2}$)x<($\frac{1}{3}$)x
p2:?x∈(0,1),log${\;}_{\frac{1}{2}}$x>log${\;}_{\frac{1}{3}}$x
p3:?x∈(0,+∞),($\frac{1}{2}$)x>log${\;}_{\frac{1}{2}}$x
p4:?x∈(0,$\frac{1}{3}$),($\frac{1}{2}$)x<log${\;}_{\frac{1}{3}}$x.
其中的真命题是( )
p1:?x∈(0,+∞),($\frac{1}{2}$)x<($\frac{1}{3}$)x
p2:?x∈(0,1),log${\;}_{\frac{1}{2}}$x>log${\;}_{\frac{1}{3}}$x
p3:?x∈(0,+∞),($\frac{1}{2}$)x>log${\;}_{\frac{1}{2}}$x
p4:?x∈(0,$\frac{1}{3}$),($\frac{1}{2}$)x<log${\;}_{\frac{1}{3}}$x.
其中的真命题是( )
| A. | p1,p3 | B. | p1,p4 | C. | p2,p3 | D. | p2,p4 |
7.若函数y=(a2+4a-5)x2-4(a-1)x+3的图象恒在x轴上方,则a的取值范围是( )
| A. | {a|1≤a≤19} | B. | {a|<a<19} | C. | {a|1≤a<19} | D. | {a|1<a≤19} |