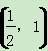题目内容
定义域为[－1,1]的奇函数f(x)满足f(x)＝f(x－2)，且当x∈(0,1)时，f(x)＝2x＋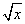
.
(1)求f(x)在[－1,1]上的解析式；
(2)求函数f(x)的值域．
解 (1)当x＝0时，f(0)＝－f(0)，故f(0)＝0.
当x∈(－1,0)时，－x∈(0,1)，
f(x)＝－f(－x)＝－(－2x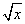＋)＝2x－.
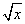若x＝－1时，f(－1)＝－f(1)．
又f(1)＝f(1－2)＝f(－1)，故f(1)＝－f(1)，得f(1)＝0，从而f(－1)＝－f(1)＝0.
综上，f(x)＝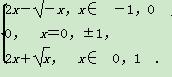
(2)∵x∈(0,1)时，f(x)＝2x＋，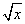
∴f′(x)＝2＋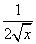
＞0，故f(x)在(0,1)上单调递增．
∴f(x)∈(0,3)．
∵f(x)是定义域为[－1,1]上的奇函数，且f(0)＝f(1)＝f(－1)＝0，
∴当x∈[－1,1]时，f(x)∈(－3,3)．
∴f(x)的值域为(－3,3)．
练习册系列答案
阅读快车系列答案
相关题目
B．y＝x，x∈{0,1}
B．±
，且方程f(x)＝0的两个实根之差等于7，则此二次函数的解析式是____________________．
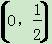B.