题目内容
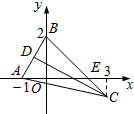 如图所示,已知△ABC中,点D是边AB的中点,边BC与x轴交于点E,∠BEA=45°.求:
如图所示,已知△ABC中,点D是边AB的中点,边BC与x轴交于点E,∠BEA=45°.求:(1)直线AB的方程;
(2)直线BC的方程;
(3)直线CD的方程.
考点:直线的一般式方程
专题:直线与圆
分析:(1)由图求出A、B的坐标,代入截距式再化为一般式方程;
(2)根据∠BEA=45°求出直线BC的倾斜角和斜率,代入斜截式再化为一般式方程;
(3)先求出C的坐标,再求出中点D的坐标,代入两点式再化为一般式方程.
(2)根据∠BEA=45°求出直线BC的倾斜角和斜率,代入斜截式再化为一般式方程;
(3)先求出C的坐标,再求出中点D的坐标,代入两点式再化为一般式方程.
解答:
解:(1)由图可知A(-1,0),B(0,2),
代入截距式得直线AB的方程为
+
=1,化为一般式得2x-y+2=0…(3分)
(2)因为∠BEA=45°,所以直线BC的倾斜角为180°-45°=135°,
所以kBC=tan135°=-1,
又B(0,2),由斜截式得直线BC的方程为y=-x+2,
化为一般式得x+y-2=0…(6分)
(3)把x=3代入x+y-2=0,得y=-1,即C(3,-1),
又由公式得D(-
,1),代入两点式得直线CD的方程为
=
,
化为一般式得4x+7y-5=0…(10分)
代入截距式得直线AB的方程为
| x |
| -1 |
| y |
| 2 |
(2)因为∠BEA=45°,所以直线BC的倾斜角为180°-45°=135°,
所以kBC=tan135°=-1,
又B(0,2),由斜截式得直线BC的方程为y=-x+2,
化为一般式得x+y-2=0…(6分)
(3)把x=3代入x+y-2=0,得y=-1,即C(3,-1),
又由公式得D(-
| 1 |
| 2 |
| y-1 |
| -1-1 |
x-(-
| ||
3-(-
|
化为一般式得4x+7y-5=0…(10分)
点评:本题主要考查直线的截距式方程、斜截式方程、两点式方程和一般式方程的综合应用,属于基础题.

练习册系列答案
相关题目
已知an+1=2an+1 (n=1,2…),则( )
| A、{an}为等比数列 |
| B、{an-1}为等比数列 |
| C、{an+1}为等比数列 |
| D、{2an+1}为等比数列 |