题目内容
在△ABC中,BC=20,∠BAC=45°,∠ABC=75°,则AB= .
考点:正弦定理
专题:解三角形
分析:由∠BAC与∠ABC的度数,求出∠ACB的度数,确定出sin∠ACB的值,再由sin∠BAC与BC的值,利用正弦定理即可求出AB的长.
解答:
解:∵在△ABC中,∠BAC=45°,∠ABC=75°,
∴∠ACB=60°,即sin∠ACB=
,
∵BC=20,
∴由正弦定理
=
得:AB=
=
=10
.
故答案为:10
.
∴∠ACB=60°,即sin∠ACB=
| ||
| 2 |
∵BC=20,
∴由正弦定理
| BC |
| sin∠BAC |
| AB |
| sin∠ACB |
| BCsin∠ACB |
| sin∠BAC |
20×
| ||||
|
| 6 |
故答案为:10
| 6 |
点评:此题考查了正弦定理,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
 如图是一个边长为4的正方形及扇形(见阴影部分),若随机向正方形内丢一粒豆子,则豆子落入扇形的概率是( )
如图是一个边长为4的正方形及扇形(见阴影部分),若随机向正方形内丢一粒豆子,则豆子落入扇形的概率是( )A、
| ||
B、
| ||
C、
| ||
| D、π |
已知两点M(-5,0),N(5,0),若直线上存在点P,使|PM|-|PN|=6,则称该直线为“B型直线”.给出下列直线:①y=x+1②y=2③y=
x④y=2x其中为“B型直线”的是( )
| 4 |
| 3 |
| A、①③ | B、①② | C、③④ | D、①④ |
若复数z=(m2-2m)+(m2-m-2)i (m∈R)为纯虚数,则m的值为( )
| A、0 | B、2 | C、0或2 | D、无解 |
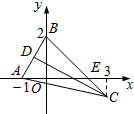 如图所示,已知△ABC中,点D是边AB的中点,边BC与x轴交于点E,∠BEA=45°.求:
如图所示,已知△ABC中,点D是边AB的中点,边BC与x轴交于点E,∠BEA=45°.求: