题目内容
设△ABC的一个顶点是A(3,-1),∠B,∠C的平分线方程分别为x=0,y=x,求直线BC的方程.
考点:直线的一般式方程
专题:直线与圆
分析:分析题意,求出A关于x=0,y=x,的对称点的坐标,都在直线BC上,利用两点式方程求解即可.
解答:
解:∵∠B、∠C的平分线分别是x=0,y=x,
∴AB与BC对于x=0对称,AC与BC对于y=x对称.
则A(3,-1)关于x=0的对称点A′(-3,-1)在直线BC上,
A关于y=x的对称点A″(-1,3)也在直线BC上,
由两点式得,
=
,
所求直线BC的方程:2x-y+5=0.
∴AB与BC对于x=0对称,AC与BC对于y=x对称.
则A(3,-1)关于x=0的对称点A′(-3,-1)在直线BC上,
A关于y=x的对称点A″(-1,3)也在直线BC上,
由两点式得,
| y-3 |
| -1-3 |
| x-(-1) |
| -3-(-1) |
所求直线BC的方程:2x-y+5=0.
点评:本题是基础题,考查点关于直线对称点的求法,直线方程的求法,考查计算能力,发现问题解决问题的能力,常考题型.

练习册系列答案
相关题目
已知两点M(-5,0),N(5,0),若直线上存在点P,使|PM|-|PN|=6,则称该直线为“B型直线”.给出下列直线:①y=x+1②y=2③y=
x④y=2x其中为“B型直线”的是( )
| 4 |
| 3 |
| A、①③ | B、①② | C、③④ | D、①④ |
定义在[-1,1]上的偶函数f(x)在[-1,0]上是减函数,已知α,β是锐角三角形的两个内角,则f(sinα)与f(cosβ)的大小关系是( )
| A、f(sinα)>f(cosβ) |
| B、f(sinα)<f(cosβ) |
| C、f(sinα)=f(cosβ) |
| D、f(sinα)与f(cosβ)的大小关系不确定 |
4张软盘与5张光盘的价格之和不小于20元,而6张软盘与3张光盘的价格之和不大于24元,则买3张软盘与9张光盘至少需要( )
| A、15元 | B、27元 |
| C、36元 | D、72元 |
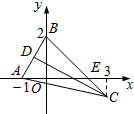 如图所示,已知△ABC中,点D是边AB的中点,边BC与x轴交于点E,∠BEA=45°.求:
如图所示,已知△ABC中,点D是边AB的中点,边BC与x轴交于点E,∠BEA=45°.求: