题目内容
已知函数F(x)=(x2-ax+1)ex,直线l:y=2x+b,其中a,b∈R.
(1)若曲线y=F(x)在点(0,F(0))处的切线为l,求a,b的值;
(2)求函数F(x)的单调递增区间;
(3)若函数F(x)在区间(0,2)上不单调,求a得取值范围.
(1)若曲线y=F(x)在点(0,F(0))处的切线为l,求a,b的值;
(2)求函数F(x)的单调递增区间;
(3)若函数F(x)在区间(0,2)上不单调,求a得取值范围.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由F′(0)=1-a=2,F(0)=1=b.
(2)令F′(x)≥0,则x2+(2-a)x+1-a≥0,化为(x+1)[x+(1-a)]≥0,对a分类讨论即可得出.
(3)由于函数F(x)在区间(0,2)上不单调,可得F′(x)=0在区间(0,2)上有解.可得a=x+1.
即可解出.
(2)令F′(x)≥0,则x2+(2-a)x+1-a≥0,化为(x+1)[x+(1-a)]≥0,对a分类讨论即可得出.
(3)由于函数F(x)在区间(0,2)上不单调,可得F′(x)=0在区间(0,2)上有解.可得a=x+1.
即可解出.
解答:
解:(1)F′(x)=(x2+(2-a)x+1-a)ex,∴F′(0)=1-a=2,解得a=-1.
F(0)=1=b,∴a=-1,b=1.
(2)令F′(x)≥0,则x2+(2-a)x+1-a≥0,化为(x+1)[x+(1-a)]≥0,
当当a=0时,化为(x+1)2≥0,此时函数F(x)在R上单调递增;
当a<0时,-1>a-1,解得x≥-1或x≤a-1,此时函数F(x)单调递增区间为(-∞,a-1],[-1,+∞);
当a>0时,-1<a-1,解得x≤-1或x≥a-1,此时函数F(x)单调递增区间为(-∞,-1],[a-1,+∞);
(3)∵函数F(x)在区间(0,2)上不单调,
∴F′(x)=0在区间(0,2)上有解.
∴x2+(2-a)x+1-a=0,
化为a=x+1.
∴1<a<3.
∴a得取值范围是(1,3).
F(0)=1=b,∴a=-1,b=1.
(2)令F′(x)≥0,则x2+(2-a)x+1-a≥0,化为(x+1)[x+(1-a)]≥0,
当当a=0时,化为(x+1)2≥0,此时函数F(x)在R上单调递增;
当a<0时,-1>a-1,解得x≥-1或x≤a-1,此时函数F(x)单调递增区间为(-∞,a-1],[-1,+∞);
当a>0时,-1<a-1,解得x≤-1或x≥a-1,此时函数F(x)单调递增区间为(-∞,-1],[a-1,+∞);
(3)∵函数F(x)在区间(0,2)上不单调,
∴F′(x)=0在区间(0,2)上有解.
∴x2+(2-a)x+1-a=0,
化为a=x+1.
∴1<a<3.
∴a得取值范围是(1,3).
点评:本题考查了利用导数研究函数的单调性极值、利用导数的几何意义研究切线,考查了推理能力与计算能力,属于难题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
执行如图的程序框图,如果输入的N是6,那么输出的p是( )


| A、120 | B、720 |
| C、1440 | D、5040 |
已知两点M(-5,0),N(5,0),若直线上存在点P,使|PM|-|PN|=6,则称该直线为“B型直线”.给出下列直线:①y=x+1②y=2③y=
x④y=2x其中为“B型直线”的是( )
| 4 |
| 3 |
| A、①③ | B、①② | C、③④ | D、①④ |
若复数z=(m2-2m)+(m2-m-2)i (m∈R)为纯虚数,则m的值为( )
| A、0 | B、2 | C、0或2 | D、无解 |

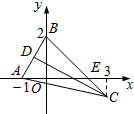 如图所示,已知△ABC中,点D是边AB的中点,边BC与x轴交于点E,∠BEA=45°.求:
如图所示,已知△ABC中,点D是边AB的中点,边BC与x轴交于点E,∠BEA=45°.求: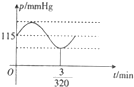 心脏跳动时,血压在增加或减小,血压的最大值和最嚣张分别成为收缩压和舒张压,当读数为120/80mmHg为标准值(收缩压为120mmHg舒张压为80mmHg)设某人的血压满足函数关系式p(t)=a+bsinωt(其中p(t)为血压(mmHg),t为事件(mim)a,b,ω为正常数),其函数图象如图所示,点(
心脏跳动时,血压在增加或减小,血压的最大值和最嚣张分别成为收缩压和舒张压,当读数为120/80mmHg为标准值(收缩压为120mmHg舒张压为80mmHg)设某人的血压满足函数关系式p(t)=a+bsinωt(其中p(t)为血压(mmHg),t为事件(mim)a,b,ω为正常数),其函数图象如图所示,点(