题目内容
已知△ABC的三条边分别为a,b,c求证:
>
.
| a+b |
| 1+a+b |
| c |
| 1+c |
考点:不等式的证明,不等式的基本性质
专题:不等式的解法及应用
分析:设f(x)=
,x∈(0,+∞),利用函数单调性的定义可得其单调递增,利用其单调性即可证明.
| x |
| 1+x |
解答:
证明:设f(x)=
,x∈(0,+∞),
设x1,x2是(0,+∞)上的任意两个实数,且x2>x1≥0,
则f(x1)-f(x2)=
-
=
,
∵x2>x1≥0,∴f(x1)<f(x2).
∴f(x)=
在(0,+∞)上是增函数.
由a+b>c>0可得f(a+b)>f(c).
即
>
.
| x |
| 1+x |
设x1,x2是(0,+∞)上的任意两个实数,且x2>x1≥0,
则f(x1)-f(x2)=
| x1 |
| 1+x1 |
| x2 |
| 1+x2 |
| x1-x2 |
| (1+x1)(1+x2) |
∵x2>x1≥0,∴f(x1)<f(x2).
∴f(x)=
| x |
| 1+x |
由a+b>c>0可得f(a+b)>f(c).
即
| a+b |
| 1+a+b |
| c |
| 1+c |
点评:本题考查了通过构造函数利用其单调性证明不等式的方法,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
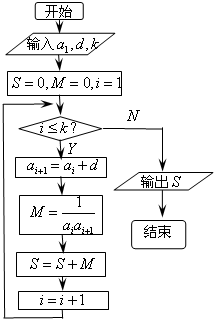 已知数列{an}的各项均为正数,观察程序框图,当k=2时,S=
已知数列{an}的各项均为正数,观察程序框图,当k=2时,S=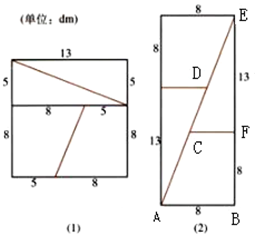 魔术大师把一块长和宽都是13dm的地毯按图(1)裁好,再按图(2)拼成矩形.计算两个图形的面积,分别得到169dm2与168dm2.魔术师得意洋洋的说,他证明了169=168.你能揭穿魔术师的奥秘吗?
魔术大师把一块长和宽都是13dm的地毯按图(1)裁好,再按图(2)拼成矩形.计算两个图形的面积,分别得到169dm2与168dm2.魔术师得意洋洋的说,他证明了169=168.你能揭穿魔术师的奥秘吗?