题目内容
已知集合M={x|y=ln（x-2）+
，x∈R}，N={x||x-1|-|4-x|＜a，x∈R}，若M∩N≠∅，则实数a的取值范围是 ．
| 3 | x-3 |
考点：交集及其运算
专题：集合
分析：求出M中x的范围确定出M，根据M与N的交集不为空集，由M中x的范围分类讨论x范围，化简N中绝对值不等式，求出a的范围即可．
解答：
解：由M中y=ln（x-2）+
，得到x-2＞0，即x＞2，
∴M={x|x＞2}，
由N中|x-1|-|4-x|＜a，M∩N≠∅，
分两种情况考虑：
当2＜x＜4时，变形得：x-1-4+x＜a，即x＜
，
要使M∩N≠∅，需
＞2，即a＞-1；
当x＞4时，变形得：x-1-x+4＜a，即a＞3，
综上，a的范围为{a|a＞-1}．
故答案为：{a|a＞-1}
| 3 | x-3 |
∴M={x|x＞2}，
由N中|x-1|-|4-x|＜a，M∩N≠∅，
分两种情况考虑：
当2＜x＜4时，变形得：x-1-4+x＜a，即x＜
| a+5 |
| 2 |
要使M∩N≠∅，需
| a+5 |
| 2 |
当x＞4时，变形得：x-1-x+4＜a，即a＞3，
综上，a的范围为{a|a＞-1}．
故答案为：{a|a＞-1}
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
智能训练练测考系列答案
相关题目
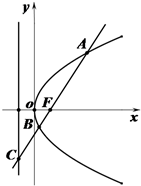如图，过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=6，则此抛物线的方程为