题目内容
甲乙丙三人独立地破译一份密码，他们每人译出此密码的概率为0.25，假定随机变量x表示译出此密码的人数，求E（x），D（x）．
考点：离散型随机变量的期望与方差
专题：概率与统计
分析：由已知条件推导出X～B（3，0.25），由此能求出结果．
解答：
解：由题意知X～B（3，0.25），
∴E（X）=3×0.25=0.75，
D（X）=3×0.25×（1-0.25）=0.5625．
∴E（X）=3×0.25=0.75，
D（X）=3×0.25×（1-0.25）=0.5625．
点评：本题考查离散型随机变量的期望和方差的求法，是基础题，解题的关键是判断出X～B（3，0.25）．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
相关题目
某几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
| B、π | ||
C、
| ||
| D、2π |
已知在一个120°的二面角的棱上有两个点A、B，AC、BD分别是在这个二面角的两个半平面内且垂直于AB的线段，又AB=4cm，AC=6cm，BD=8cm，则CD的长为（ ）
A、2
| ||
B、
| ||
C、2
| ||
D、4
|
已知△ABC的两顶点坐标A（-1，0），B（1，0），圆E是△ABC的内切圆，在边AC，BC，AB上的切点分别为P，Q，R，|CP|=1（从圆外一点到圆的两条切线段长相等），动点C的轨迹为曲线M．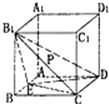
如图，正方体ABCD-A1B1C1D1中，E是AB的中点