题目内容
 已知△ABC的两顶点坐标A(-1,0),B(1,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=1(从圆外一点到圆的两条切线段长相等),动点C的轨迹为曲线M.
已知△ABC的两顶点坐标A(-1,0),B(1,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=1(从圆外一点到圆的两条切线段长相等),动点C的轨迹为曲线M.(I)求曲线M的方程;
(Ⅱ)设直线BC与曲线M的另一交点为D,当点A在以线段CD为直径的圆上时,求直线BC的方程.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(I)由题意,可得曲线M是以A,B为焦点,长轴长为4的椭圆(挖去与x轴的交点),从而可得求曲线M的方程;
(Ⅱ)设与直线BC的方程,与椭圆方程联立,消x,利用韦达定理,结合
•
=0,即可求直线BC的方程.
(Ⅱ)设与直线BC的方程,与椭圆方程联立,消x,利用韦达定理,结合
| AC |
| AD |
解答:
解:(I)由题知|CA|+|CB|=|CP|+|CQ|+|AP|+|BQ|=2|CP|+|AB|=4>|AB|,
所以曲线M是以A,B为焦点,长轴长为4的椭圆(挖去与x轴的交点),
所以a=2,c=1,
所以b=
,
所以曲线M:
+
=1(y≠0)为所求.---------------(4分)
(Ⅱ)注意到直线BC的斜率不为0,且过定点B(1,0),

设直线BC的方程为x=my+1,C(x1,y1),D(x2,y2),
与椭圆方程联立,消x得(4+3m2)y2+6my-9=0,
所以y1+y2=-
,y1y2=-
-------------------------------------(8分)
因为
=(my1+2,y1),
=(my2+2,y2),
所以
•
=(my1+2)(my2+2)+y1y2=
注意到点A在以CD为直径的圆上,所以
•
=0,即m=±
,-----(11分)
所以直线BC的方程3x+
y-3=0或3x-
y-3=0为所求.------(12分)
所以曲线M是以A,B为焦点,长轴长为4的椭圆(挖去与x轴的交点),
所以a=2,c=1,
所以b=
| 3 |
所以曲线M:
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)注意到直线BC的斜率不为0,且过定点B(1,0),

设直线BC的方程为x=my+1,C(x1,y1),D(x2,y2),
与椭圆方程联立,消x得(4+3m2)y2+6my-9=0,
所以y1+y2=-
| 6m |
| 3m2+4 |
| 9 |
| 3m2+4 |
因为
| AC |
| AD |
所以
| AC |
| AD |
| 7-9m2 |
| 3m2+4 |
注意到点A在以CD为直径的圆上,所以
| AC |
| AD |
| ||
| 3 |
所以直线BC的方程3x+
| 7 |
| 7 |
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知F是双曲线
-
=1(a>0)的右焦点,O为坐标原点,设P是双曲线C上一点,则∠POF的大小不可能是( )
| x2 |
| 3a2 |
| y2 |
| a2 |
| A、15° | B、25° |
| C、60° | D、165° |
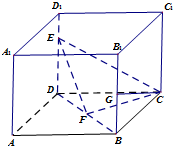 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱DD1上的动点,F,G分别是BD,BB1的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱DD1上的动点,F,G分别是BD,BB1的中点. 如图,已知四边形ABCD与CDEF均为正方形,平面ABCD⊥平面CDEF.
如图,已知四边形ABCD与CDEF均为正方形,平面ABCD⊥平面CDEF.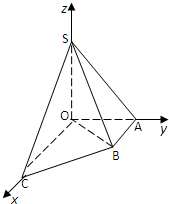 如图直角梯形OABC中,∠COA=∠OAB=90°,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,分别以OC,OA,OS为x轴、y轴、z轴建立直角坐标系O-xyz.
如图直角梯形OABC中,∠COA=∠OAB=90°,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,分别以OC,OA,OS为x轴、y轴、z轴建立直角坐标系O-xyz.