题目内容
已知在一个120°的二面角的棱上有两个点A、B，AC、BD分别是在这个二面角的两个半平面内且垂直于AB的线段，又AB=4cm，AC=6cm，BD=8cm，则CD的长为（ ）
A、2
| ||
B、
| ||
C、2
| ||
D、4
|
考点：向量在几何中的应用,平面向量数量积的坐标表示、模、夹角,多面体和旋转体表面上的最短距离问题,与二面角有关的立体几何综合题
专题：计算题,平面向量及应用,空间位置关系与距离
分析：由已知可得
=
+
+
，
•
=0，
•
=0，利用数量积的性质即可得出．
| CD |
| CA |
| AB |
| BD |
| CA |
| AB |
| AB |
| BD |
解答：
解：由条件，知
•
=0，
•
=0，
=
+
+
．
所以|
|2=|
|2+|
|2+|
|2+2
•
+2
•
+2
•
=62+42+82+2×6×8cos60°=164
所以CD=2
cm，
故选C．
| CA |
| AB |
| AB |
| BD |
| CD |
| CA |
| AB |
| BD |
所以|
| CD |
| CA |
| AB |
| BD |
| CA |
| AB |
| AB |
| BD |
| CA |
| BD |
=62+42+82+2×6×8cos60°=164
所以CD=2
| 41 |
故选C．
点评：本题考查面面角，考查空间距离的计算，熟练掌握向量的运算和数量积运算是解题的关键．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
己知某几何体的三视图如图所示，则该几何体的体积是（ ）
A、
| ||||
B、
| ||||
C、2
| ||||
D、2
|
已知F是双曲线
-
=1(a＞0)的右焦点，O为坐标原点，设P是双曲线C上一点，则∠POF的大小不可能是（ ）
| x2 |
| 3a2 |
| y2 |
| a2 |
| A、15° | B、25° |
| C、60° | D、165° |
函数y=ln（x+1）与y=
的图象交点的横坐标所在区间为（ ）
| 1 |
| x |
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
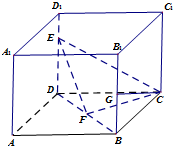如图，在棱长为1的正方体ABCD-A1B1C1D1中，点E是棱DD1上的动点，F，G分别是BD，BB1的中点．
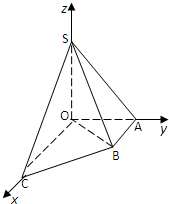如图直角梯形OABC中，∠COA=∠OAB=90°，OC=2，OA=AB=1，SO⊥平面OABC，SO=1，分别以OC，OA，OS为x轴、y轴、z轴建立直角坐标系O-xyz．
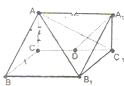已知三棱柱ABC-A1B1C1的底面为直角三角形，则棱与底面垂直，如图所示，D是棱CC1的中点，且∠ACB=90°，BC=1，AC=