题目内容
17.已知F是抛物线y2=2px(p>0)的焦点,过F的直线与抛物线交于A、B两点,AB中点为C,过C作抛物线的准线的垂线交准线于C1点,若CC1中点M的坐标为($\sqrt{2}$,4),则p=4$\sqrt{2}$.分析 先设A,B的坐标,根据A,B满足抛物线方程将其代入得到两个关系式,再将两个关系式相减根据直线的斜率,求出AB的方程,代入抛物线方程,利用纵坐标的值可求出p的值.
解答 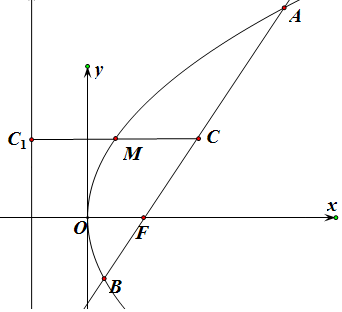 解:设A(x1,y1)、B(x2,y2),则其准线为x=-$\frac{p}{2}$
解:设A(x1,y1)、B(x2,y2),则其准线为x=-$\frac{p}{2}$
∵CC1中点M的坐标为($\sqrt{2}$,4),∴y1+y2=8,
C(2$\sqrt{2}$+$\frac{p}{2}$,4),F($\frac{P}{2}$,0),可得AB的斜率为:$\sqrt{2}$,
AB的方程为:y=$\sqrt{2}$(x-$\frac{p}{2}$),
代入抛物线方程可得:y2-$\sqrt{2}$py-p2=0
∴y1+y2=$\sqrt{2}p$,
可得$\sqrt{2}$p=8,
∴p=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 本题考查抛物线的几何性质、直线与抛物线的位置关系等基础知识.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
8.若函数f(x)的定义域为[1,2],则函数y=f(x2)的定义域为( )
| A. | [1,4] | B. | [1,$\sqrt{2}$] | C. | [-$\sqrt{2}$,$\sqrt{2}$] | D. | [-$\sqrt{2}$,-1]∪[1,$\sqrt{2}$] |
5.在△ABC中,若$\frac{cosA}{cosB}=\frac{b}{a}$,则△ABC是( )
| A. | 等腰或直角三角形 | B. | 等边三角形 | ||
| C. | 直角三角形 | D. | 等腰三角形 |
2.若三点A(0,8),B(-4,0),C(m,-4)共线,则实数m的值是( )
| A. | 6 | B. | -2 | C. | -6 | D. | 2 |
 如图,在平行六面体ABCD-A1B1C1D1中,M,N分别在面对角线AC,A1C上且CM=2MA,A1N=2ND.记向量$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,\overrightarrow{A{A_1}}=\overrightarrow c$,用$\overrightarrow a,\overrightarrow b,\overrightarrow c$表示$\overrightarrow{MN}$.
如图,在平行六面体ABCD-A1B1C1D1中,M,N分别在面对角线AC,A1C上且CM=2MA,A1N=2ND.记向量$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,\overrightarrow{A{A_1}}=\overrightarrow c$,用$\overrightarrow a,\overrightarrow b,\overrightarrow c$表示$\overrightarrow{MN}$.