题目内容
设(5x-
)n的展开式的各项系数之和为M,二项式系数之和为N,M-N=240,求展开式中x3项的系数.
| x |
考点:二项式系数的性质
专题:二项式定理
分析:由条件求得n=4,在二项展开式的通项公式中,令x的幂指数等于,3,求出r的值,即可求得展开式中x3项的系数.
解答:
解:由题意可得N=2n,令x=1,则M=(5-1)n=4n=(2n)2.
∴(2n)2-2n=240,2n=16,n=4.
(5x-
)n=(5x-
)4的展开式中第r+1项Tr+1=C
•(5x)4-r•(-
)r
=(-1)r•C
•54-r•x4-
.
令4-
=3,即r=2,可得展开式中x3项的系数为 C
•52•(-1)2=150.
∴(2n)2-2n=240,2n=16,n=4.
(5x-
| x |
| x |
r 4 |
| x |
=(-1)r•C
r 4 |
| r |
| 2 |
令4-
| r |
| 2 |
2 4 |
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
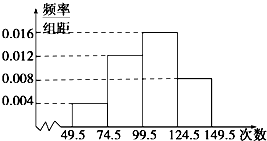 为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知如图:第一小组的频数为5.
为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知如图:第一小组的频数为5.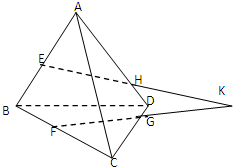 如图,三棱锥A-BCD中,E、F分别是棱AB、BC的中点,H、G分别是棱AD、CD上的点,且EH∩FG=K.求证:
如图,三棱锥A-BCD中,E、F分别是棱AB、BC的中点,H、G分别是棱AD、CD上的点,且EH∩FG=K.求证: