题目内容
15.已知定义域为R的函数 f (x)的导函数为f'(x),且满足f'(x)-2f (x)>4,若 f (0)=-1,则不等式f(x)+2>e2x的解集为( )| A. | (0,+∞)?? | B. | (-1,+∞)?? | C. | (-∞,0)? | D. | (-∞,-1) |
分析 根据条件构造函数F(x)=$\frac{f(x)+2}{{e}^{2x}}$,求函数的导数,利用函数的单调性即可得到结论.
解答 解:设F(x)=$\frac{f(x)+2}{{e}^{2x}}$,
则F′(x)=$\frac{f′(x)-2f(x)-4}{{e}^{2x}}$,
∵f(x)-2f′(x)-4>0,
∴F′(x)>0,即函数F(x)在定义域上单调递增,
∵f(0)=-1,∴F(0)=1,
∴不等式f(x)+2>e2x等价为不等式 $\frac{f(x)+2}{{e}^{2x}}$>1等价为F(x)>F(0),
解得x>0,
故不等式的解集为(0,+∞),
故选:A.
点评 本题主要考查函数单调性的判断和应用,根据条件构造函数是解决本题的关键.

练习册系列答案
相关题目
5.《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为( )
| A. | $\frac{10}{11}$升 | B. | $\frac{65}{66}$升 | C. | $\frac{67}{66}$升 | D. | $\frac{37}{33}$升 |
10.设复数z1=1+2i,z2=2-i,i为虚数单位,则z1z2=( )
| A. | 4+3i | B. | 4-3i | C. | -3i | D. | 3i |
20.执行图中程序框图,若输入x1=2,x2=3,x3=7,则输出的T值为( )
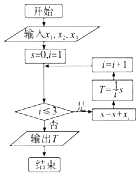

| A. | 3 | B. | 4 | C. | $\frac{11}{3}$ | D. | 5 |
7.双曲线C:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1的离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}}{4}$ |
4.设数列{an}满足:a1=2,an+1=1-$\frac{1}{{a}_{n}}$,记数列{an}的前n项之积为T,则T2017的值为( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | 2 | D. | -2 |