题目内容
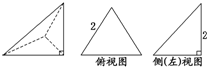 已知三棱锥的直观图及其俯视图与侧(左)视图如图,俯视图是边长为2的正三角形,侧(左)视图是有一直角边为2的直角三角形,则该三棱锥的正(主)视图面积为
已知三棱锥的直观图及其俯视图与侧(左)视图如图,俯视图是边长为2的正三角形,侧(左)视图是有一直角边为2的直角三角形,则该三棱锥的正(主)视图面积为考点:简单空间图形的三视图
专题:常规题型
分析:先根据俯视图与侧视图进一步确定原三棱锥中边的方位及边与边的长度关系,然后画出正视图,即可求得其面积.
解答:
 解:由题意可知,原三棱锥S-ABC的底面三角形△ABC是边长为2的正三角形,边AB为横向放置,高为SB,
解:由题意可知,原三棱锥S-ABC的底面三角形△ABC是边长为2的正三角形,边AB为横向放置,高为SB,
于是得正视图是直角边长为2的等腰直角三角形,如右图所示,
其面积S=
×2×2=2.
故答案为2.
 解:由题意可知,原三棱锥S-ABC的底面三角形△ABC是边长为2的正三角形,边AB为横向放置,高为SB,
解:由题意可知,原三棱锥S-ABC的底面三角形△ABC是边长为2的正三角形,边AB为横向放置,高为SB,于是得正视图是直角边长为2的等腰直角三角形,如右图所示,
其面积S=
| 1 |
| 2 |
故答案为2.
点评:本题既要根据三视图想象几何体的形状,又要根据几何体的形状画出三视图,主要考查了学生的逆向思维能力和空间想象力由于只涉及到简单平面图形的计算,所以对计算的要求不高,属容易题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在线性回归模型中,下列叙述正确的是( )
| A、比较两个模型的拟合效果,可以通过比较它们的残差平方和的大小来确定,残差平方和越大的模型,拟合效果越好 |
| B、在残差图中,残差点所在的带状区域的宽度越窄,拟合效果越好 |
| C、在残差图中,残差点所在的带状区域的宽度越宽,拟合效果越好 |
| D、通过回归方程得到的预报值就是预报变量的精确值 |
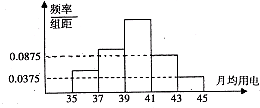 某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如图所示;其中直方图从左到右前3个小矩形的面积之比为1:2:3.该乡镇月均用电量在37~39之内的居民共有
某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如图所示;其中直方图从左到右前3个小矩形的面积之比为1:2:3.该乡镇月均用电量在37~39之内的居民共有 用红、黄、蓝、绿、黑5种颜色给如图的a、b、c、d四个区域染色,若相邻的区域不能用相同的颜色,不同的染色方法的种数有
用红、黄、蓝、绿、黑5种颜色给如图的a、b、c、d四个区域染色,若相邻的区域不能用相同的颜色,不同的染色方法的种数有