题目内容
已知异面直线a,b均与平面α相交,下列命题:①存在直线m?α,使得m⊥a或m⊥b; ②存在直线m?α,使得m⊥a且m⊥b; ③存在直线m?α,使得m与a和b所成的角相等.其中不正确的命题为 .
考点:命题的真假判断与应用
专题:空间位置关系与距离,简易逻辑
分析:由于异面直线a,b均与平面α相交,因此一定存在平面β∥γ,使得a?β,b?γ.
①利用直线与直线的位置关系即可判断出,;
②只有β⊥α时才正确;
③利用线面角的定义即可判断出.
①利用直线与直线的位置关系即可判断出,;
②只有β⊥α时才正确;
③利用线面角的定义即可判断出.
解答:
解:由于异面直线a,b均与平面α相交,因此一定存在平面β∥γ,使得a?β,b?γ.
①存在直线m?α,使得m⊥a或m⊥b,正确;
②存在直线m?α,使得m⊥a且m⊥b,不一定正确,只有β⊥α时才正确;
③存在直线m?α,使得m与a和b所成的角相等,正确.
故答案为:②.
①存在直线m?α,使得m⊥a或m⊥b,正确;
②存在直线m?α,使得m⊥a且m⊥b,不一定正确,只有β⊥α时才正确;
③存在直线m?α,使得m与a和b所成的角相等,正确.
故答案为:②.
点评:本题考查了异面直线的性质、线面位置关系、线线角、简易逻辑的判定,考查了举反例否定一个命题的方法,考查了推理能力,属于基础题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
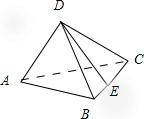 在四面体ABCD中,已知
在四面体ABCD中,已知| AB |
| b |
| AD |
| a |
| AC |
| c |
| BE |
| 1 |
| 2 |
| EC |
| DE |
A、-
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
在四边形ABCD中,M、N分别是AD和BC的中点,则向量
=( )
| MN |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
在△ABC中,若
<0,则△ABC的形状是( )
| a2+c2-b2 |
| 2ac |
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不能确定 |