题目内容
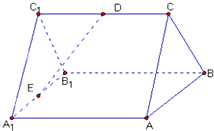 如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点,E为底面一边A1B1的中点.
如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点,E为底面一边A1B1的中点.(Ⅰ)求证:AB⊥DF;
(Ⅱ)求三棱锥A1-ABD的体积,并求直线A1B1到与它平行的平面DAB的距离.
考点:直线与平面垂直的性质,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(Ⅰ)取AB中点F,连EF,DF,则EF⊥AB,由已知条件推导出DF⊥AB,由此能证明AB⊥DF.
(Ⅱ)由已知条件得VA1-ABD=VD-A1BA=
×h×S△ABA1=
,设直线A1B1到与它平行的平面DAB的距离d.利用等积法能求出三棱锥A1-ABD的体积,求出直线A1B1到与它平行的平面DAB的距离.
(Ⅱ)由已知条件得VA1-ABD=VD-A1BA=
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
解答:
解:(Ⅰ)取AB中点F,连EF,DF,则EF⊥AB,
ABC-A1B1C1是正三棱柱,D为侧棱CC1的中点,
∴DA=DB,∴DF⊥AB,
∴AB⊥平面DEF,∴AB⊥DF.(4分)
(Ⅱ)∵ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,
D为侧棱CC1的中点,E为底面一边A1B1的中点,
∴VA1-ABD=VD-A1BA=
×h×S△ABA1=
,(8分)
由题意知DA=DB=
,∴S△AED=2,
设直线A1B1到与它平行的平面DAB的距离d.
∵VA1-ABD=VD-A1BA=
,
∴
×d×S△ABD=
×d×2=
,
∴d=
.(12分)
ABC-A1B1C1是正三棱柱,D为侧棱CC1的中点,
∴DA=DB,∴DF⊥AB,

∴AB⊥平面DEF,∴AB⊥DF.(4分)
(Ⅱ)∵ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,
D为侧棱CC1的中点,E为底面一边A1B1的中点,
∴VA1-ABD=VD-A1BA=
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
由题意知DA=DB=
| 5 |
设直线A1B1到与它平行的平面DAB的距离d.
∵VA1-ABD=VD-A1BA=
| 2 |
| 3 |
| 3 |
∴
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
∴d=
| 3 |
点评:本题考查异面直线垂直的证明,考查三棱锥体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知
=2
,
=3
,
=4
,
=5
,…
=10
,则推测a+b=( )
2+
|
|
3+
|
|
4+
|
|
5+
|
|
10+
|
|
| A、1033 | B、109 |
| C、199 | D、29 |