题目内容
已知向量
，
满足
=-
，|
|=2，|
|=3，则
•
=（ ）
| a |
| b |
| a |
| 2 |
| 3 |
| b |
| a |
| b |
| a |
| b |
| A、-9 | B、-6 | C、6 | D、9 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：将
=-
，带入
•
，再根据
2=|
|2即可求出答案．
| a |
| 2 |
| 3 |
| b |
| a |
| b |
| b |
| b |
解答：
解：
•
=(-
)•
=-
2=-6．
故选：B．
| a |
| b |
| 2 |
| 3 |
| b |
| b |
| 2 |
| 3 |
| b |
故选：B．
点评：将
=-
带入
•
求解，或根据数量积的运算公式
•
=|
||
|cosπ，注意向量
，
的夹角是π．
| a |
| 2 |
| 3 |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
练习册系列答案
相关题目
如图，椭圆的中心在坐标原点O，顶点分别为A1，A2，B1，B2，焦点分别为F1，F2，延长B1F2与A2B2交于P点，若∠B1PB2为锐角，则此椭圆离心率e的取值范围是一个平面将一个半径为2的实心球截为两个部分，且截面经过球心，那么每个部分的表面积为（ ）
| A、12π | B、16π |
| C、4π | D、8π |
若P=
+
，Q=
+
（a≥0），则P，Q的大小关系为（ ）
| a+2 |
| a+5 |
| a+3 |
| a+4 |
| A、P＞Q | B、P=Q |
| C、P＜Q | D、由a的取值确定 |
若函数f(x)=
(a，b，c，d∈R)的图象如图所示，则a：b：c：d=（ ）
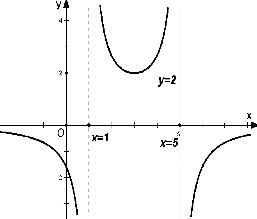
| d |
| ax2+bx+c |
| A、1：6：5：8 |
| B、1：6：5：（-8） |
| C、1：（-6）：5：8 |
| D、1：（-6）：5：（-8） |
若方程x2+（a+2）y2+2ax+a=0表示圆，则a的值为（ ）
| A、-1 | B、2 |
| C、-1或2 | D、不存在 |
已知数列{an}的前n项和为Sn，且Sn=n2+2n+1，则a3+a4+a5=（ ）
| A、11 | B、16 | C、27 | D、32 |
228与1995的最大公约数为（ ）
| A、57 | B、39 | C、46 | D、58 |
用反证法证明：某方程“方程有唯一解”中，假设正确的是该方程（ ）
| A、无解 | B、有两个解 |
| C、至少两解 | D、至少有两个解或无解 |