题目内容
用反证法证明：某方程“方程有唯一解”中，假设正确的是该方程（ ）
| A、无解 | B、有两个解 |
| C、至少两解 | D、至少有两个解或无解 |
考点：反证法与放缩法
专题：推理和证明
分析：根据命题“方程有唯一解”的否定为“至少有两个解或无解”，从而得出结论．
解答：
解：由于命题“方程有唯一解”的否定为“至少有两个解或无解”，
故用反证法证明命题“方程有唯一解”时，应假设至少有两个解或无解，
故选：D．
故用反证法证明命题“方程有唯一解”时，应假设至少有两个解或无解，
故选：D．
点评：解此题关键要懂得反证法的意义及步骤．在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，不需要一一否定，只需否定其一即可．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
已知向量
，
满足
=-
，|
|=2，|
|=3，则
•
=（ ）
| a |
| b |
| a |
| 2 |
| 3 |
| b |
| a |
| b |
| a |
| b |
| A、-9 | B、-6 | C、6 | D、9 |
如图，可作为函数y=f（x）的图象是（ ）
A、 |
B、 |
C、 |
D、 |
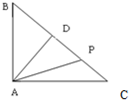如图，已知△ABC中，AB=3，AC=4，BC=5，AD⊥BC于D点，点P为BC边所在直线上的一个动点，则| AP |
| AD |
| A、最大值为9 | ||
B、为定值
| ||
| C、最小值为3 | ||
| D、与P的位置有关 |
一个口袋中装有m个白球，n个黑球，从口袋中每次拿一个球不放回，第k次拿到黑球的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
以下关于几何体的三视图的讨论中，正确的是（ ）
| A、球的三视图总是三个全等的圆 |
| B、正方体的三视图总是三个全等的正方形 |
| C、水平放置的正四面体的三视图都是正三角形 |
| D、水平放置的圆台的俯视图是一个圆 |
已知f（x）是定义在R上的偶函数，且在（-∞，0）内是增函数，f（1）=0，若f（x）＜0，则实数x的取值范围是（ ）
| A、（-1，0）∪（0，1） |
| B、（-∞，-1）∪（0，1） |
| C、（-1，0）∪（1，+∞） |
| D、（-∞，-1）∪（1，+∞） |
函数y=f（x-4）的图象与函数y=f（2-x）的图象关于下列哪条直线对称（ ）
| A、x=3 | B、x=-1 |
| C、x=1 | D、x=-3 |