题目内容

228与1995的最大公约数为（　　）
A、57B、39C、46D、58
考点：用辗转相除计算最大公约数
专题：算法和程序框图
分析：根据辗转相除法：用较大的数字除以较小的数字，得到商和余数，然后再用上一式中的除数和得到的余数中较大的除以较小的，以此类推，当整除时，就得到要求的最大公约数．
解答： 解：∵1995÷228=8…171，
228÷171=1…57，
172÷57=3，
∴228与1995的最大公约数是57，
故选：A．
点评：本题考查了辗转相除法求最大公约数的运用，属于基础题，熟练掌握辗转相除法求最大公约数的方法和步骤是解答本题的关键．
练习册系列答案
相关题目
求（1+x+x2+x3）（1-x）7的展开式中x4的系数
 
．
已知向量
a
，
b
满足
a
=-
2
3
b
，|
a
|=2，|
b
|=3，则
a
•
b
=（　　）
A、-9B、-6C、6D、9
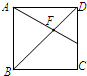如图，正方形ABCD的边长为3，E为DC的中点，AE与BD相交于F，则
FD
•
DE
的值是（　　）
A、
3
2
B、3
C、-
3
2
D、-3
定义集合A与B的运算“*”为：A*B={x|x∈A或x∈B，但x∉A∩B}．设X是偶数集，Y={1，2，3，4，5}，则（X*Y）*Y=（　　）
A、XB、YC、X∩YD、X∪Y
计算机中常用的十六进制是逢16进1的记数制，采用数字0-9和字母A-F共16个记数符号；这些符号与十进制的数的对应关系如下表：
十六进制0123456789ABCDEF
十进制0123456789101112131415
例如，用十六进制表示：E+D=1B，则A×E=（　　）
A、6EB、8CC、5FD、82
如图，可作为函数y=f（x）的图象是（　　）
A、
B、
C、
D、
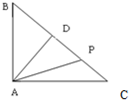如图，已知△ABC中，AB=3，AC=4，BC=5，AD⊥BC于D点，点P为BC边所在直线上的一个动点，则
AP
•
AD
满足（　　）
A、最大值为9
B、为定值
144
25
C、最小值为3
D、与P的位置有关
函数y=f（x-4）的图象与函数y=f（2-x）的图象关于下列哪条直线对称（　　）
A、x=3B、x=-1
C、x=1D、x=-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网