题目内容
已知数列{an}的前n项和为Sn，且Sn=n2+2n+1，则a3+a4+a5=（ ）
| A、11 | B、16 | C、27 | D、32 |
考点：数列的求和
专题：点列、递归数列与数学归纳法
分析：根据数列项an与Sn之间的关系即可得到结论．
解答：
解：∵数列{an}的前n项和为Sn，且Sn=n2+2n+1，
∴a3+a4+a5=S5-S2=（52+2×5+1）-（22+2×2+1）=27，
故选：C
∴a3+a4+a5=S5-S2=（52+2×5+1）-（22+2×2+1）=27，
故选：C
点评：本题主要考查数列项的计算，根据项an与Sn之间的关系是解决本题的关键．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
已知a
+b
=1，则以下成立的是（ ）
| 1-b2 |
| 1-a2 |
| A、a2+b2＞1 |
| B、a2+b2=1 |
| C、a2+b2＜1 |
| D、a2b2=1 |
已知向量
，
满足
=-
，|
|=2，|
|=3，则
•
=（ ）
| a |
| b |
| a |
| 2 |
| 3 |
| b |
| a |
| b |
| a |
| b |
| A、-9 | B、-6 | C、6 | D、9 |
对于z=（
）100+（
）200，下列结论成立的是（ ）
| 1+i | ||
|
| 1-i | ||
|
| A、z是零 | B、z是纯虚数 |
| C、z是正实数 | D、z是负实数 |
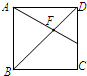如图，正方形ABCD的边长为3，E为DC的中点，AE与BD相交于F，则| FD |
| DE |
A、
| ||
| B、3 | ||
C、-
| ||
| D、-3 |
如图，可作为函数y=f（x）的图象是（ ）
A、 |
B、 |
C、 |
D、 |
已知f（x）是定义在R上的偶函数，且在（-∞，0）内是增函数，f（1）=0，若f（x）＜0，则实数x的取值范围是（ ）
| A、（-1，0）∪（0，1） |
| B、（-∞，-1）∪（0，1） |
| C、（-1，0）∪（1，+∞） |
| D、（-∞，-1）∪（1，+∞） |