题目内容
在等比数列{an}中,an>0(n∈N*),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,又a3与a5的等比中项为2.
(1) 求数列{an}的通项公式;
(2) 设bn=log2an,求数列{bn}的前n项和Sn;
(3) 是否存在k∈N*,使得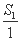 +
+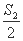 +…+
+…+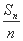 <k对任意n∈N*恒成立?若存在,求出k的最小值;若不存在,请说明理由.
<k对任意n∈N*恒成立?若存在,求出k的最小值;若不存在,请说明理由.
(1) 因为a1a5+2a3a5+a2a8=25,{an}为等比数列,
所以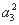 +2a3a5+
+2a3a5+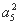 =25,所以(a3+a5)2=25.
=25,所以(a3+a5)2=25.
又an>0,所以a3+a5=5,又a3与a5的等比中项为2,
所以a3a5=4,而q∈(0,1),
所以a3>a5,所以a3=4,a5=1,所以q=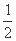 ,a1=16,
,a1=16,
所以an=16×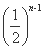 =25-n.
=25-n.
(2) 因为bn=log2an=log225-n5-n,
所以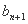 -bn=-1,b1=log2a1=log216=log224=4.
-bn=-1,b1=log2a1=log216=log224=4.
所以{bn}是以4为首项、-1为公差的等差数列,所以Sn=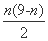 .
.
(3) 由(2)知Sn=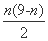 ,所以
,所以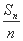 =
=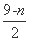 .
.
当n≤8时,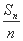 >0;当n=9时,
>0;当n=9时,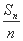 =0;当n>9时,
=0;当n>9时,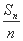 <0.
<0.
所以当n=8或9时,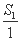 +
+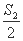 +
+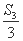 +…+
+…+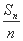 =18最大.
=18最大.
故存在k∈N*,使得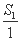 +
+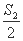 +…+
+…+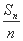 <k对任意n∈N*恒成立,k的最小值为19.
<k对任意n∈N*恒成立,k的最小值为19.

练习册系列答案
相关题目
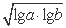 ,Q=
,Q=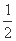 (lga+lgb),R=lg
(lga+lgb),R=lg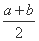 ,求P,Q,R的大小关系.
,求P,Q,R的大小关系.
 A1B1C1中,点D是BC的中点.
A1B1C1中,点D是BC的中点.
 为等差数列,若
为等差数列,若 <-1,且它们的前n项和Sn有最大值,则使得Sn>0的n的最大值为 .
<-1,且它们的前n项和Sn有最大值,则使得Sn>0的n的最大值为 . 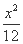 +
+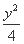 =1在第一象限内的一点P(x,y)分别作x轴、y轴的两条垂线,垂足分别为M,N,求矩形PMON的周长最大值时点P的坐标.
=1在第一象限内的一点P(x,y)分别作x轴、y轴的两条垂线,垂足分别为M,N,求矩形PMON的周长最大值时点P的坐标.