题目内容
8.已知抛物线y2=4$\sqrt{3}$x的准线与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)相交于A,B两点,双曲线的一条渐近线方程是y=$\sqrt{2}$x,点F是抛物线的焦点,且△FAB是正三角形,则双曲线的标准方程是${x^2}-\frac{y^2}{2}=1$.分析 抛物线y2=4$\sqrt{3}$x的焦点为F($\sqrt{3}$,0),其准线方程为x=-$\sqrt{3}$,利用△FAB为正三角形,可得A的坐标,代入双曲线的方程,可得a,b的方程,利用双曲线的一条渐近线方程是y=$\sqrt{2}$x,可得a,b的方程,从而可得a,b的值,即可求出双曲线的方程.
解答 解:抛物线y2=4$\sqrt{3}$x的焦点为F($\sqrt{3}$,0),其准线方程为x=-$\sqrt{3}$,
∵△FAB为正三角形,
∴|AB|=4,
将(-$\sqrt{3}$,2)代入双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1可得$\frac{3}{{a}^{2}}-\frac{4}{{b}^{2}}$=1,
∵双曲线的一条渐近线方程是y=$\sqrt{2}$x,∴$\frac{b}{a}$=$\sqrt{2}$,
∴a=1,b=$\sqrt{2}$,
∴双曲线C2的方程为${x^2}-\frac{y^2}{2}=1$.
故答案为${x^2}-\frac{y^2}{2}=1$.
点评 本题考查抛物线、双曲线的方程与性质,考查学生的计算能力,正确运用抛物线、双曲线的性质是关键.

练习册系列答案
相关题目
16.若Sn=sin$\frac{π}{7}$+sin$\frac{2π}{7}$+…+sin$\frac{nπ}{7}$(n∈N+),则在S1,S2,…,S2017中,值为零的个数是( )
| A. | 143 | B. | 144 | C. | 287 | D. | 288 |
3.已知等差数列{an}中,a1=11,a5=-1,则{an}的前n项和Sn的最大值是( )
| A. | 15 | B. | 20 | C. | 26 | D. | 30 |
13.过点(1,2)且与直线y=2x+1垂直的直线的方程为( )
| A. | x+2y-3=0 | B. | 2x-y+4=0 | C. | x+2y+3=0 | D. | x+2y-5=0 |
20.已知△ABC的三边长为a,b,c,满足直线ax+by+2c=0与圆x2+y2=4相离,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | ||
| C. | 钝角三角形 | D. | 以上情况都有可能 |
17.已知全集U=R,集合A={x|x2+x-6>0},B={y|y≤3},则(∁UA)∩B=( )
| A. | [-3,3] | B. | [-1,2] | C. | [-3,2] | D. | (-1,2] |
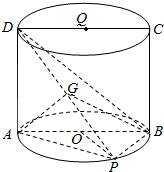 如图,四边形ABCD是体积为8$\sqrt{3}$π的圆柱OQ的轴截面,点P在底面圆周上,BP=OA=2,G是DP的中点.
如图,四边形ABCD是体积为8$\sqrt{3}$π的圆柱OQ的轴截面,点P在底面圆周上,BP=OA=2,G是DP的中点.