题目内容
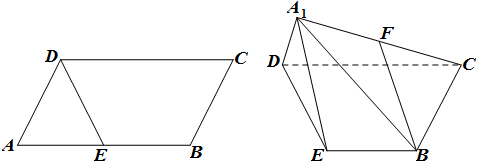
已知平行四边形ABCD,AB=4,AD=2,∠DAB=60°,E为AB的中点,把三角形ADE沿DE折起至A1DE位置,使得A1C=4,F是线段A1C的中点.
(1)求证:BF∥面A1DE;
(2)求证:面A1DE⊥面DEBC;
(3)求四棱锥A1-DEBC的体积.

(1)求证:BF∥面A1DE;
(2)求证:面A1DE⊥面DEBC;
(3)求四棱锥A1-DEBC的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)取DA1的中点G,连接FG、GE,通过证明BF∥EG,利用直线与平面平行的判定定理证明BF∥平面A1DE.
(2)取DE的中点H,连接A1H、CH,通过证明A1H⊥面DEBC,然后通过平面与平面垂直的判定定理证明面A1DE⊥面DEBC.
(3)利用(2)的结果,直接求解几何体的体积即可.
(2)取DE的中点H,连接A1H、CH,通过证明A1H⊥面DEBC,然后通过平面与平面垂直的判定定理证明面A1DE⊥面DEBC.
(3)利用(2)的结果,直接求解几何体的体积即可.
解答:
(本题14分)
解:(1)证明:取DA1的中点G,连接FG、GE,
∵F为A1C中点,

∴GF∥DC,且GF=
DC,
∵E为平行四边形ABCD边AB的中点,
∴EB∥DC,且EB=
DC,
∴EB∥GF,且EB=GF,
∴四边形BFGE是平行四边形,
∴BF∥EG,
∵EG?平面A1DE,BF?平面A1DE
∴BF∥平面A1DE…(4分)
(2)取DE的中点H,连接A1H、CH,
∵AB=4,AD=2,∠DAB=60°,E为AB的中点,
∴△DAE为等边三角形,即折叠后△DA1E也为等边三角形,
∴A1H⊥DE,且A1H=
,

在△DHC中,DH=1,DC=4,∠HDC=60°
根据余弦定理,可得HC2=DH2+DC2-2DH•DCcos60o=12+42-2×1×4×
=13,
在△A1HC中,A1H=
,HC=13,A1C=4,
∴A1C2=A1H2+HC2,即A1H⊥HC
又∵
,所以A1H⊥面DEBC
又∵A1H?面A1DE∴面A1DE⊥面DEBC…(10分)
(3)由第(2)问知A1H⊥面DEBC,
VA1-DEBC=
S底面DEBC•h=
×
(2+4)×
×
=3…(14分)
解:(1)证明:取DA1的中点G,连接FG、GE,
∵F为A1C中点,

∴GF∥DC,且GF=
| 1 |
| 2 |
∵E为平行四边形ABCD边AB的中点,
∴EB∥DC,且EB=
| 1 |
| 2 |
∴EB∥GF,且EB=GF,
∴四边形BFGE是平行四边形,
∴BF∥EG,
∵EG?平面A1DE,BF?平面A1DE
∴BF∥平面A1DE…(4分)
(2)取DE的中点H,连接A1H、CH,
∵AB=4,AD=2,∠DAB=60°,E为AB的中点,
∴△DAE为等边三角形,即折叠后△DA1E也为等边三角形,
∴A1H⊥DE,且A1H=
| 3 |

在△DHC中,DH=1,DC=4,∠HDC=60°
根据余弦定理,可得HC2=DH2+DC2-2DH•DCcos60o=12+42-2×1×4×
| 1 |
| 2 |
在△A1HC中,A1H=
| 3 |
∴A1C2=A1H2+HC2,即A1H⊥HC
又∵
|
又∵A1H?面A1DE∴面A1DE⊥面DEBC…(10分)
(3)由第(2)问知A1H⊥面DEBC,
VA1-DEBC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查直线与平面平行与垂直的判定定理,平面与平面垂直的判定定理的应用,几何体的体积的求法,考查空间想象力以及计算能力.

练习册系列答案
相关题目
设Sn为等比数列{an}的前n项和,27a2+a5=0,则
=( )
| S4 |
| S2 |
| A、10 | B、-5 | C、9 | D、-8 |
执行算法代码“For I From 1 To 99 Step 2”共执行的循环次数为( )
| A、49 | B、50 | C、51 | D、52 |
曲线x2-3y2=0与双曲线C:
-
=1(a>0,b>0)的四个交点与C的两个虚轴顶点构成一个正六边形,则双曲线C的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|



