题目内容
设集合M={1，2，3}的非空真子集个数是（ ）
| A、6 | B、7 | C、8 | D、9 |
考点：子集与真子集
专题：集合
分析：根据集合子集的公式2n（其中n为集合中的元素的个数），求出集合A的子集个数，然后除去本身和空集即可得到集合A的非空真子集的个数．
解答：
解：因为集合A中有3个元素，所以集合A子集有23=8个，则集合A的非空真子集的个数是8-2=6．
故选A．
故选A．
点评：此题考查学生掌握子集与真子集的定义，会利用2n-2求集合的非空真子集，是一道基础题．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
设集合M={x|x≥-1}，N={x|x≤k}，若M∩N≠￠，则k的取值范围是（ ）
| A、（-∞，-1] |
| B、[-1，+∞） |
| C、（-1，+∞） |
| D、（-∞，-1） |
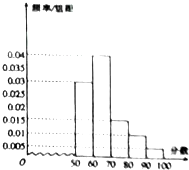在一次物理竞赛中，学生成绩均在内[50，100），相应的频率分布直方图如图，已知成绩在[60，70）的学生有40人，则成绩在[70，90）的人数为（ ）