题目内容
15.已知正三棱锥D-ABC侧棱两两垂直,E为棱AD中点,平面α过点A,且α∥平面EBC,α∩平面ABC=m,α∩平面ACD=n,则m,n所成角的余弦值是$\frac{\sqrt{10}}{5}$.分析 利用面面平行的性质可得m∥BC,n∥CE,故∠BCE即为所求角,设棱锥侧棱长为1,利用余弦定理计算cos∠BCE.
解答 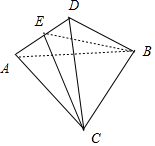 解:∵α∥平面EBC,α∩平面ABC=m,平面EBC∩平面ABC=BC,
解:∵α∥平面EBC,α∩平面ABC=m,平面EBC∩平面ABC=BC,
∴m∥BC,
同理可得:n∥CE,
∴∠BCE为直线m,n所成的角.
设正三棱锥的侧棱为1,则BC=$\sqrt{2}$,CE=BE=$\frac{\sqrt{5}}{2}$,
在△BCE中,由余弦定理得:cos∠BCE=$\frac{\frac{5}{4}+2-\frac{5}{4}}{2•\frac{\sqrt{5}}{2}•\sqrt{2}}$=$\frac{\sqrt{10}}{5}$.
故答案为:$\frac{{\sqrt{10}}}{5}$.
点评 本题考查了面面平行的性质,空间角的计算,属于中档题.

练习册系列答案
相关题目
6. 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败.
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败.
(Ⅰ)求图中a的值;
(Ⅱ)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(Ⅲ)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的分布列与数学期望E(X).
(参考公式:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败.
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败.| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | ||
| 女 | 50 | ||
| 合计 |
(Ⅱ)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(Ⅲ)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的分布列与数学期望E(X).
(参考公式:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| P(K2≥k0) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
9.已知$sin(\frac{π}{3}-α)=\frac{1}{4}$,则$cos(\frac{π}{3}+2α)$=( )
| A. | $\frac{5}{8}$ | B. | $-\frac{7}{8}$ | C. | $-\frac{5}{8}$ | D. | $\frac{7}{8}$ |