题目内容
5.已知点A(1,0),B(4,0),圆C:(x-a)2+(y-a)2=1,若圆C上存在点M,使|MB|=2|MA|,则实数a的取值范围为-$\frac{\sqrt{6}}{2}$≤a≤-$\frac{\sqrt{2}}{2}$或$\frac{\sqrt{2}}{2}$≤a≤$\frac{\sqrt{6}}{2}$.分析 由圆C上存在点M,使|MB|=2|MA|,得到点M在以D(0,0)为圆心,以2为半径的圆上,圆C与圆D有公共点,满足2-1≤CD≤2+1,即可求出a的取值范围.
解答 解:由C:(x-a)2+(y-a)2=1,得圆心C(a,a),
设M(x,y),
∵|MB|=2|MA|,
∴(x-4)2+y2=4(x-1)2+4y2,
得x2+y2=4.
∴点M在以D(0,0)为圆心,以2为半径的圆上,
则圆C与圆D有公共点,满足2-1≤CD≤2+1,
即1≤a2+a2≤3,
解得-$\frac{\sqrt{6}}{2}$≤a≤-$\frac{\sqrt{2}}{2}$或$\frac{\sqrt{2}}{2}$≤a≤$\frac{\sqrt{6}}{2}$.
故答案为-$\frac{\sqrt{6}}{2}$≤a≤-$\frac{\sqrt{2}}{2}$或$\frac{\sqrt{2}}{2}$≤a≤$\frac{\sqrt{6}}{2}$.
点评 本题考查圆的标准方程,考查了两圆间位置关系的应用,体现了数学转化思想方法,考查不等式组的解法,是中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
10.在△ABC中,A:B:C=4:1:1,则a:b:c=( )
| A. | 4:1:1 | B. | 2:1:1 | C. | 3:1:1 | D. | $\sqrt{3}$:1:1 |
17.已知函数$f(x)=\frac{{{x^2}-2x}}{x-2},g(x)=\sqrt{1+x}+\sqrt{1-x}$,下列判断正确的是( )
| A. | 函数f(x)是奇函数,函数g(x)是偶函数 | |
| B. | 函数f(x)不是奇函数,函数g(x)是偶函数 | |
| C. | 函数f(x)是奇函数,函数g(x)不是偶函数 | |
| D. | 函数f(x)不是奇函数,函数g(x)不是偶函数 |
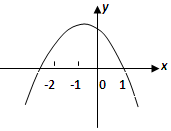 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0; ②b2-4ac>0;③4a-2b+c>0; ④a-b+c<0
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0; ②b2-4ac>0;③4a-2b+c>0; ④a-b+c<0