题目内容
11.若函数$f(x)=\sqrt{{2^{a{x^2}-2ax-1}}-1}$的定义域为R,则实数a的取值范围是∅.分析 根据函数$f(x)=\sqrt{{2^{a{x^2}-2ax-1}}-1}$的定义域为R,得出${2}^{{ax}^{2}-2ax-1}$-1≥0恒成立,化为ax2-2ax-1≥0恒成立,即$\left\{\begin{array}{l}{a>0}\\{△={4a}^{2}-4a×(-1)≤0}\end{array}\right.$,解不等式组即可.
解答 解:函数$f(x)=\sqrt{{2^{a{x^2}-2ax-1}}-1}$的定义域为R,
∴${2}^{{ax}^{2}-2ax-1}$-1≥0恒成立,
即${2}^{{ax}^{2}-2ax-1}$≥1恒成立,
∴ax2-2ax-1≥0恒成立;
即$\left\{\begin{array}{l}{a>0}\\{△={4a}^{2}-4a×(-1)≤0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a>0}\\{-1≤a≤0}\end{array}\right.$,
即a∈∅;
∴实数a的取值范围是∅.
故答案为:∅.
点评 本题考查了求函数定义域的应用问题,也考查了不等式恒成立的问题,是基础题.

练习册系列答案
相关题目
16.过抛物线y=2x2的焦点F作倾斜角为120°的直线交抛物线于A、B两点,则弦|AB|的长为( )
| A. | 2 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
1.若$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(3,4),则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值( )
| A. | $-\frac{{2\sqrt{5}}}{25}$ | B. | $\frac{{2\sqrt{5}}}{25}$ | C. | $2\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
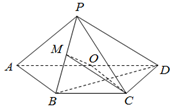 如图,在四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点.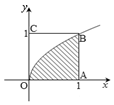 如图,在正方形OABC内任取一点,取到函数$y=\sqrt{x}$的图象与x轴正半轴之间
如图,在正方形OABC内任取一点,取到函数$y=\sqrt{x}$的图象与x轴正半轴之间